八年级数学竞赛试题
 (时间120分钟,满分120分)
(时间120分钟,满分120分)
一、填空题(每小题3分,共30分)
1、8l的平方根为____________
2、已知点 P 在第二象限,它的横坐标与纵坐标的和为1,则点 P 的坐标是________.
(写出符合条件的一个点即可)
3、一个多边形的内角和为12600 ,则它的边数是____________.
4、已知![]() (
(![]() 是正整数)且
是正整数)且![]() 那么
那么![]() 的值是
的值是
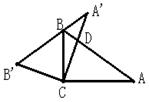 5、如图,在Rt△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A’B’C的位置,其中A’、B’分别是A、B的对应点,且点B在斜边A’B’上,直角边CA’交AB于点D,则∠DCA的度数_____。
5、如图,在Rt△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A’B’C的位置,其中A’、B’分别是A、B的对应点,且点B在斜边A’B’上,直角边CA’交AB于点D,则∠DCA的度数_____。
6、小王与同学约好下午4:30在学校门口见,不见不散,为此,他们在早上8:00钟两人均把自己的表对准,小王于4:30正点走到学校门口,可是同学没来,原来同学的手表比正确时间每小时慢4分钟,如果同学按他自己的手表4:30到达,则小王还要等 分钟(正确时间)
 7、甲、乙两位探险者到沙漠进行探险。某日早晨7∶00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进。上午10∶00,甲、乙二人的距离的平方是_____。
7、甲、乙两位探险者到沙漠进行探险。某日早晨7∶00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进。上午10∶00,甲、乙二人的距离的平方是_____。
8、一个等腰三角形的周长为16,底边上的高是4,则
这个三角形的三边长分别是______,_____,_______。
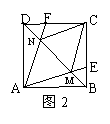
9、已知:如图2,E、F分别是正方形ABCD的边BC、
CD上的点,AE、AF分别与对角线BD相交于M、N,
 若∠EAF=500,则∠CME +∠CNF = ________。
若∠EAF=500,则∠CME +∠CNF = ________。
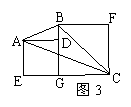
10、如图3,将面积为![]() 的正方形与面积为
的正方形与面积为![]() 的正方形
的正方形
(b>a)放在一起,则△ABC的面积是__________。
二、选择题(每小题3分,共30分)
1、ΔABC 中三边之比为1:
1: ![]() ,则ΔABC 形状一定不是 (
)
,则ΔABC 形状一定不是 (
)
A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、锐角三角形
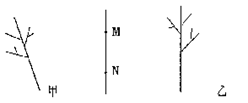 2、.将图4中的图案甲变成图案乙,正确的说法是 ( )
2、.将图4中的图案甲变成图案乙,正确的说法是 ( )
A、“扶正”后即可
B、“扶正”后向右平移即可
C、“扶正”后作直线 MN 的轴对称图形即可
D、以上三种方法都可
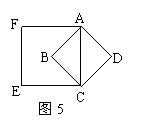 3、如图5,正方形ABCD的边长为1cm,以对角线AC为边长再作一个正方形,则正方形ACEF的面积是( )
3、如图5,正方形ABCD的边长为1cm,以对角线AC为边长再作一个正方形,则正方形ACEF的面积是( )
A、3cm2 B、4cm2 C、5cm2 D、2cm2
4、以线段![]() 为边,
为边,
 且使a∥c作四边形,这样的四边形( )
且使a∥c作四边形,这样的四边形( )
A、能作两个 B、能作三个 C、能作无数个 D、不能作
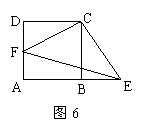
5、如图6,正方形的面积为256,点F在AD上,点E在AB的延长线上,Rt△CEF的面积为200,则BE的值为( )
A、10 B、11 C、12 D、15
6、实数a、b满足ab =1,若![]() ,
,
 则M、N的关系为( )
则M、N的关系为( )
A、M>N B、M=N C、M<N D、不确定
7、一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如左图),那么B点从开始至结束走过的路径长度为( )
A、![]() B、
B、![]() C、 4 D、2 +
C、 4 D、2 +![]()
8、在甲组图形的4个图中,每个图示由4种简单图形A、B、C、D(不同的线段或圆)
中的某两个图形组成的,例如由A、B组成的图形记为![]() ,在乙组图形的(a)、(b)、 (c)、(d)4个图中,表示“
,在乙组图形的(a)、(b)、 (c)、(d)4个图中,表示“![]() ”和“
”和“![]() ”的是( )
”的是( )
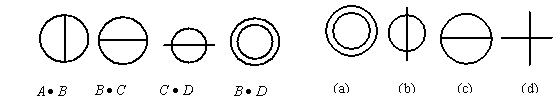 |
A、 (a),(b) B、 (b),(c) C、 (c),(d) D、 (b),(d)
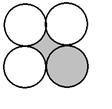 9、如图所示的4个的半径均为1,那么图中的阴影部分的
9、如图所示的4个的半径均为1,那么图中的阴影部分的
面积为( )
A、![]() B、
B、![]()
![]() C、 4 D、6
C、 4 D、6
10、正ΔABC的顶点A、B 的坐标分别为A (0,0),B(2,0),则点C 的坐标为 ( )
A、(1,![]() ) B、(1,-
) B、(1,- ![]() )
)
C、(1,![]() ) 或(1,-
) 或(1,-![]() )
D、(-1,
)
D、(-1,![]() ) 或 (-1,-
) 或 (-1,-![]() )
)
三、(每题10分, 计30分)
1、已知四边形ABCD中 ,AB=AD,∠BAD=60°,∠BCD=120°,请说明:BC+DC=AC
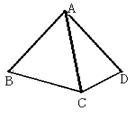
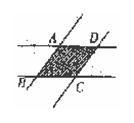
2、如图,两条等宽的长纸条倾斜地重叠着, 试说明重叠部分ABCD为菱形.
 |
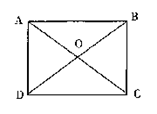 3、已知:四边形 ABCD,从下列给出的条件中任取 (个数不限) 几个组合,使四边形ABCD为矩形,并说明理由.(写出两种组合)
3、已知:四边形 ABCD,从下列给出的条件中任取 (个数不限) 几个组合,使四边形ABCD为矩形,并说明理由.(写出两种组合)
① AB// CD ② AD // BC ③ AB= CD
④ AO = CO = BO =DO ⑤∠ABC =∠DCB
⑥ AC =2 AB ⑦AC =BD ⑧AO = CO,BO =DO
四、(每题15分, 计30分)
4、如图, 已知正方形ABCD的对角线AC、BD 相交于点O ,E 是AC 上一点,过 A 作AG ⊥EB,垂足为G,AG 交 BD 于点 F,则 OE=OF.(对上述命题,可证 RtΔBOE ≌ Rt ΔAOF,可得OE=OF.) 若点 E 在 AC 的延长线上,AG ⊥ EB 交 EB的延长线于点 G,AG的延长线交 DB的延长线于点F,其他条件不变,则结论“OE = OF ”还成立吗 ? 如果成立,请说明理由;如果不成立,也请说明理由.
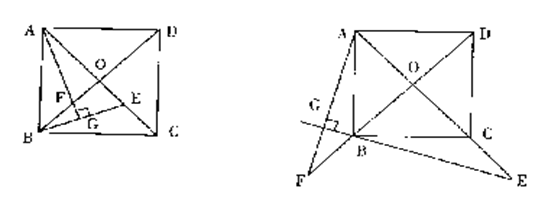
![]() 5、ΔABC中,
∠C=900,
∠A, ∠B, ∠C
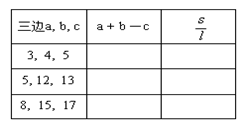
的对边分别为 a, b, c,设A4BC的面积为s,周长为
l ,探索 与
a + b-c 的值之间的关系.
5、ΔABC中,
∠C=900,
∠A, ∠B, ∠C
的对边分别为 a, b, c,设A4BC的面积为s,周长为
l ,探索 与
a + b-c 的值之间的关系.
(1)计算后填表: (6分)
(2) 观察分析后猜想: 若设 a + b-c = m(m为正实数), 则 =_________.(用m表示). (4分)
(3) 写出(2)中结论的推导过程.(5分)
八年级数学竞赛答案
一、填空题。
1、±9 2、(略) 3、9 4、16 5、70 6、![]() 7、
424
7、
424
8、 5,5,6 9、 1000 10、 ![]()
二、选择题
D、C、D、E、D、B、B、D、C、C
三、
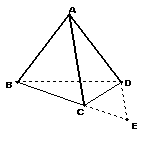 1、已知四边形ABCD中 ,AB=AD,∠BAD=60°,∠BCD=120°,请说明:BC+DC=AC
1、已知四边形ABCD中 ,AB=AD,∠BAD=60°,∠BCD=120°,请说明:BC+DC=AC
由AB=AD,∠BAD=60°可得![]() 是等边三角形,
是等边三角形,
把![]() 绕点D逆时针旋转60°,点A与点B重合,
绕点D逆时针旋转60°,点A与点B重合,
点C转到点E,连接EC,则![]() 是等边三角形,
是等边三角形,
∠BAD=60°,又因为∠BCD=120°,
所以∠BAD+∠BCD=180°,故B、C、
E共线,
所以AC=BE=BC+CE=BC+DC
2-3、(略)
四、
4-5 (略)