八年级数学科期中考试卷
| 题号 | 一 | 二、三 | 四 | 五 | 六 | 总分 |
| 得分 |
|
|
|
|
|
|
一、填空题（每小题3分，共30分）
1．已知函数
，当
时，函数值为 ；
2． 函数
的自变量
的取值范围是
；
3．直线
向上平移2个单位，所得直线的解析式是
；
4．对八年级(6)班60名同学的一次数学单元测试成绩进行统计，如果频数分布直方图中80.5~90.5分这一组的频数是15，那么这个班的学生这次数学测试成绩在80.5~90.5分之间的频率是 ；
5．如图1，⊿
≌⊿
，则
；
 |
(1) (2) (3)
6．如图2，要测量河两岸相对的两点A，B的距离，在AB的垂线BF上取两点C，D，使BC＝CD，再定出BF的垂线DE，使A，C，E在一条直线上，这时只要测量两点 的距离，就能得到A，B的距离；
7．分析数据时，为了能表示出每个项目的具体数目，我们常选用_________图；
8．如图3，在世界人口扇形统计图中，关于中国部分的圆心角的度数为 度。
9．某地的电话月租费20元，通话费每分钟0.15元，则每月话费y（元）与通话时间x（分钟）之间的关系式是 ；
10. 小王调查“每人每天的用水量”这一问题时，收集到80个数据，最大数据是60升，最小数据是40升，若取组距为4，则应分为_________组绘制频数分布表．
二、选择题:（每小题3分，共15分）
11. 一天，小明从达濠西园坐车到汕头新华书店买书，然后步行到人民广场，最后乘16路公共汽车回到西园，下图中能体现他离西园的距离y（千米）与时间x（时）的关系的图象是（ ）
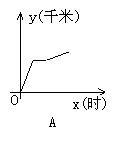
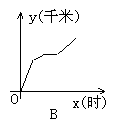
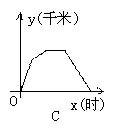
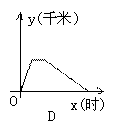
12．一次函数
的图象经过（ ）
（A）第一、三、四象限 （B）第二、三、四象限
（C）第一、二、三象限 （D）第一、二、四象限
13．如图，已知
，
，下列条件中不能判定⊿
≌⊿
的是（ ）
（A）
（B）
（C）
（D）
∥
（第13题）
14．在某扇形统计图中，其中某一部分扇形面积所对的圆心角是
，那么它所代表的部分占总体的（ ）
（A）
（B）
（C）
（D）
15．右图中两条直线
和
和交点坐标
可以看作下列方程组中（ ）的解。
（A）
（B）
（C）
（D）
三、（本小题9分）
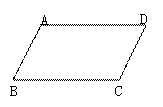
17．如图，在四边形ABCD中AB=CD，AD=BC，那么AB∥CD；AD∥BC．
你能应用本学期所学的知识说明其中的道理吗？
四、解答、证明题（每小题8分，共16分）
18、已知一次函数
的图象经过点A（1，6）及点B（-2，0）.
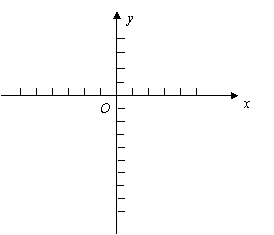（1）求此一次函数的解析式，并画出函数图象。
（2）此函数图象与
轴交于A，与
轴交于B,
求此函数图象与坐标轴围成的三角形的面积S .
19．为加强公民的节水意识，某城市制定了以下用水收费标准：每户每月用水未超过20立方米时，每立方米收费2.0元，超过20立方米的部分每立方米收费2.8元，设某户每月用水量为x (立方米)，应交水费为y (元)
①分别写出用水未超过20立方米和多于20立方米时，y与x间的函数关系式；
②如果某用户某月共交水费59.6元，求这个月该用户用水多少立方米？
五、（每小题8分，共16分）
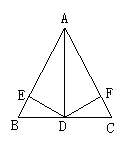
20．已知：如图，在△ABC中，AD平分∠BAC，BD＝CD，DE⊥AB于E，DF⊥AC
于F，且AE=AF.
求证：①
②
21、为了了解某校七年级男生的体能情况，从该校七年级抽取50名男生进行
1分钟跳绳测试，把所得数据整理后，画出频数分布直方图（如图）．
已知图中从左到右第一、第二、第三、第四小组的频数的比为1：3：4：2．
（1）求第二小组的频数和频率；
（2）求所抽取的50名男生中，1分钟跳绳次数在100次以上（含100次）的人数占所抽取的男生人数的百分比．
六、（每小题7分，共14分）
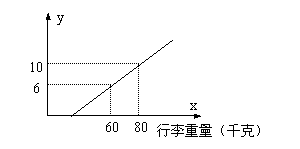22、某地长途汽车客运公司规定，旅客可随身携带一定重量的行李，如果超过规定，则需要购买行李票，行李票费用y（元）是行李重量x（千克）的一次函数，其图象如图所示。
求 ①y与x之间的函数关系式；
②旅客最多可免费携带行李的千克数。
23、北京某厂和上海某厂同时制成某大型机器若干台，北京厂可支援外地10台，上海厂可支援外地4台，现在决定给重庆8台，汉口6台。如果从北京运往汉口、重庆的运费分别是400元/台、800元/台，从上海运往汉口、重庆的运费分别是300元/台、500元/台。
求：(1)设上海运往汉口台，总运费为元，求与的函数关系式；
(2)若要求总运费不超过8200元，共有几种调运方案?
(3)求出总运费最低的调运方案，最低总运费是多少元?
八年级数学科期中考试卷参考答案
一、填空题（每小题3分，共30分）
1．7；2． 
； 3．
；4．0.25； 5．
；6．DE；
7．条形图；8．72；9． 
；10. 6．
二、选择题:（每小题3分，共15分）
11. C； 12．D；13．C； 14．A； 15．B；
三、（本小题9分）
17．解：连结AC，证明⊿
≌⊿
，得到对应角相等，从而得证；
四、解答、证明题（每小题8分，共16分）
18、（1）
；（图略）； （2）4；
19．
五、（每小题8分，共16分）
20．（1）证明⊿
≌⊿
（2）证明⊿
≌⊿
21、（1）15；0.3；（2）
六、（每小题7分，共14分）
22、（1）
；（2）30
23、
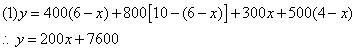
