八年级（下）期末数学测试题
班级___________ 姓名_____________.
（总分：100分，考试时间：60分钟）
考生注意：其中带※的题为升学考试要求而水平考试不要求的题目。
一、选择题（本大题8个小题，每小题4分，共32分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个答案是正确的，请选出填在题后的括号内。
1、化简
等于( )
A、
B、
C、
D、
2、计算
的结果是( )
A、
B、- C、-1
D、1
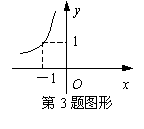
3、如右图，某个反比例函数的图象经过点P，则它的解析式为（ ）
A、
B、
C、
D、
4、已知反比例函数
的图象上有两点
、
且
，那么下列结论正确的是（ ）
A、
B、
C、
D、
与
之间的大小关系不能确定
5、等边三角形的面积为
，它的高为（ ）
A、
B、 
C、
D、
6、在△ABC中，AB＝15，AC＝13，高AD＝12，则△ABC周长为（ ）
A、42 B、32 C、42或32 D、37或33
7、已知□ABCD的周长为50cm，△ABC的周长为35cm ,则对角线AC的长为（ ）
A、5cm B、10cm C、15cm D、20cm
8、□ABCD中，∠A:∠B:∠C:∠D的值可以是（ ） www.czsx.com.cn
A、1:2:3:4 B、2:2:1:1 C、2:1:2:1 D、1:2:2:1
9、
，
，……，
的平均数为a，
，
，……，
的平均数为b，则，，……，的平均数为（ ）
A、
B、
C、
D、
10、数据10，10，
，8的众数与平均数相同，那么这组数的中位数是（ ）
A、10 B、8 C、12 D、4
※11、□ABCD中，E为BC的中点，F为EC的中点，则
：
=（ ）
A、1:4 B、1:6 C、1:8 D、1:12
※12、已知：一组数据，，
，
，
的平均数是2，方差是
，那么另一组数据3 －2，3－2，3－2，3－2，3－2的平均数和方差分别是（ ）
A、2， B、2，1 C、4，
D、4，3
二、填空题（本大题6个小题，每小题3分，共18分）在每小题中，请将答案直接写在题后横线上。 www.czsx.com.cn
13、用科学记数法表示:12.5毫克=________吨。
14、计算(x+y)·
=___________。
15、近视眼镜的度数y（度）与镜片焦距x（米）成反比例。已知400度近视眼镜镜片的焦距为0.25米，则眼镜度数y与镜片焦距x之间的函数关系式是_____________。
16、比例函数
的图像在所在象限内y随x的增大而增大，则n=
。
17、若一个三角形的三边分别为3k，4k，5k（k为自然数），则这个三角形为＿＿＿三角形。
18、设a＞b，如果a+b，a-b是三角形较小的两条边，当第三边等于＿＿＿时，这个三角形为直角三角形。
19、若□ABCD中，∠A=40°，则∠B= °，∠C= °，∠D= °。
20、若□ABCD的周长为100cm，两条对角线相交于点O，△AOB的周长比△BOC的周长多10cm，那么AB= cm，BC= cm。
21、某学生在一次考试中7科成绩的和为658，其中有两科的平均分为89，那么另外五科的平均分是________。
22、为了估计鱼塘里有多少条鱼，我们从鱼塘捕100条做上标记，然后放回鱼塘里去，经过一段时间，等带标记的鱼完全混合于鱼群后，再捕第二次样品鱼200条，若其中带标记的鱼有25条，则可估计鱼塘里约有鱼__________条。 www.czsx.com.cn
※23、如图，菱形ABCD中，DE⊥AB，垂足是E，
DE＝6，sinA＝
，则菱形ABCD的周长是 。
 |
※24、如图，在□ABCD中，两对角线交于点O，点E、F、G、H分别是AO、BO、CO、DO的中点，那么以图中的点为顶点的平行四边形有 个，请你在图中将它们画出来，它们分别是 。
三、解答题（共50分）解答时请写出必要的演算过程或推理步骤。www.czsx.com.cn
25、（8分）计算：
;
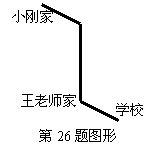
26、（7分）如图，小刚家、王老师家，学校在同一条路上，小刚家到王老师家的路程为3千米，王老师家到学校的路程为0.5千米。由于小刚的父母战斗在抗“禽流感”的第一线，为了使他能按时到校，王老师每天骑自行车接小刚上学。已知王老师骑自行车的速度是步行的3倍，每天比平时步行上班多用了20分钟，问王老师的步行速度及骑自行车的速度各是多少？
27、（8分）甲、乙两名运动员在6次百米跑训练中的成绩如下：（单位：秒）
| 甲 | 10.8 | 10.9 | 11.0 | 10.7 | 11.2 | 10.8 |
| 乙 | 10.9 | 10.9 | 10.8 | 10.8 | 10.5 | 10.9 |
请你比较这两组数据的众数、平均数、中位数，谈谈你的看法。
29、（8分）沙漠探险队的A组由驻地出发，以12公里/是垢速成度向东南方向搜索前进，同时，B组也由驻地出发，以9公里/时的速度向东北方向搜索前进。求2个小时后，A，B两组之间的距离。
※30、（8分）某单位为响应政府发出的全民健身的号召，打算在长和宽分别为20米和11米的矩形大厅内修建一个60平方米的矩形健身房ABCD。该健身房的四面墙壁中有两侧沿用大厅的旧墙壁（如图为平面示意图），已知装修旧墙壁的费用为20元/平方米，新建（含装修）墙壁的费用为80元/平方米. 设健身房的高为3米，一面旧墙壁AB的长为x米，修建健身房的总投入为y元。
（1）求y与x的函数关系式；
（2）为了合理利用大厅，要求自变量x必须满足8≤x≤12。当投入资金为4800元时，问利用旧墙壁的总长度为多少米？
※31、（10分）已知：□ABCD中，AB=6，对角线AC交BD于点O，△AOB的周长为15，求对角线AC、BD的和。
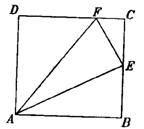※32、（10分）如图，在正方形ABCD中，E是BC的中点，F为CD上一点，且CF=
CD。
求证：△AEF是直角三角形。
答案: www.czsx.com.cn
| 选择题 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | B | D | D | C | C | B | C | D | A | C | D |
二、13、1.25×10-8；14、x+y；15、
；16、
；17、直角；
18、
；19、140°，40°，140°；20、30，20；21、96；22、800；
23、40；24、4个（包括□ABCD）；□ABCD、□EFGH、□AFCH、□BGDE；
三、25、解:原式=
=
。
26、解:设王老师步行的速度是x千米/时,则骑自行车的速度是3x千米/时, 20分钟=
小时,
由题意,得
,解得x=5.
经检验x=5是所列方程的根,∴3x=3×5=15(千米/时).
答:王老师步行的速度是5千米/时,骑自行车的速度是15千米/时。
27、甲的众数、平均数、中位数依次为：10.8 10.9 10.85
乙的众数、平均数、中位数依次为：10.9 10.8 10.85
说明：众数、平均数、中位数比较正确的一组给1分，看法合理给1分。
28、证明：∵四边形ABCD为矩形，∴AC=BD，则BO=CO。
∵BE⊥AC于E，CF⊥BD于F，∴∠BEO=∠CFO=90°。
又∵∠BOE=∠COF，∴△BOE≌△COF，∴BE=CF。
29、2个小时后，A组走的路程为：12×2=24（公里），B组走的路程为：9×2=18（公里）
因两组前进的方向是直角，所以两组之间的距离是：
=30（公里）
答：2个小时后，两组之间的距离是30公里。
30、（1）根据题意，AB=x，AB·BC=60，所以
.
，即
.
（2）当y=4800时，有
.
去分母并整理，得
.
解得
，
.
经检验，，都是原方程的根.
由8≤x≤12，只取x=10。所以利用旧墙壁的总长度为
米。
31、∵OA+OB+AB=15且AB=6 ∴OA+OB=9 又∵平行四边形ABCD互相平分
∴AC+BD=2AO+2BO=2（AO+BO）=18
32、设正方形ABCD的边长为a则，BE=CE=
a, CF=a. DF=
a
在R
△ABE中，由勾股定理得AE
=AB+BF=a+
同理在R
△ADF中，AF=AD+DF=a+
,
在R△CEF中，EF=CE+CF=
∴AF=AE+EF，∴△AEF是直角三角形。 www.czsx.com.cn