八年级数学第二学期期末复习检测试题一
一、细心择一择，你一定很准（每题2分，共24分）
1，在统计中，样本的方差可以近似地反映总体的（ ）
A.平均状态 B.波动大小 C.分布规律 D.集中趋势
2，若分式
的值为零，则x的值为（ ）
A.3 B.3或－3 C.－3 D.0
3，一件工作，甲独做a小时完成，乙独做b小时完成，则甲、乙两人合作完成需要（ ）小时
A.
B.
C.
D.
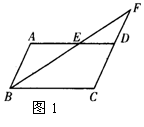
4，如图1，在□ABCD中，AB＝4cm，AD＝7cm，∠ABC平分线交AD于E，交CD的延长线于点F，则DF＝（ ）
A.2cm B.3cm C.4cm D.5cm
5，正比例函数y＝k1x（k1≠0）和反比例函数y＝
（k2≠0）的一个交点为（m，n），则另一个交点为（ ）
A.（－m，－n） B.（－m，n） C.（m，－n） D.（m，n）
6，在下列性质中，平行四边形不一定具有的是（ ）
A.对边相等 B.对边平行 C.对角互补 D.内角和为360°
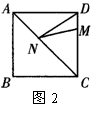
7，已知如图2，正方形ABCD的边长为8，M在DC上，且DM＝2，N是AC上的一动点，则DN+MN的最小值为（ ）
A.9 B.10
C.11 D.12
 | |||
 |
8，在一次射击练习中，甲、乙两人前5次射击的成绩分别为（单位：环）
甲：10 8 10 10 7 乙：7 10 9 9 10
则这次练习中，甲、乙两人方差的大小关系是（ ）
A.S2甲＞S2乙 B.S2甲＜S2乙 C.S2甲＝S2乙 D.无法确定
9，一鞋店试销一种新款女鞋，试销期间卖出情况如下表：
| 型号 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
| 数量（双） | 3 | 5 | 10 | 15 | 8 | 3 | 2 |
对于这个鞋店的经理来说最关心哪种型号鞋畅销，则下列统计量对鞋店经理来说最有意义的是（ ）
A.平均数 B.众数 C.中位数 D.标准差
10，等边三角形的面积为8
，它的高为（ ）
A.2
B.4
C.2
D.2
11，若方程
＝
有正数根，则k的取值范围是（ ）
A. k＜2 B. k≠－3 C.－3＜k＜2 D. k＜2且k≠－3
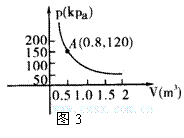
12，某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压p（kPa）是气体体积V（m3）的反比例函数，其图象如图3所示，当气球内的气压大于140kPa时，气球将爆炸，为了完全起见，气体体积应（ ）
A.不大于
m3 B.不小于m3 C.不大于
m3 D.不小于m3
二、仔细填一填，你一定很行（每题2分，共24分）
13，计算(x+y)·
＝__________.
14，比例函数y＝
的图像在所在象限内y随x的增大而增大，则n＝ .
15，若a＝
，则
的值等于________.
16，若□ABCD的周长为100cm，两条对角线相交于点O，△AOB的周长比△BOC的周长多10cm，那么AB＝ cm，BC＝ cm.
17，在Rt△ABC中，∠C＝90°，有两边长为6，8，则第三边长为_______cm.
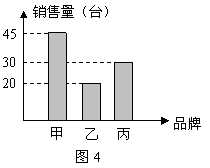18，如图4是华联商厦某个月甲、乙、丙三种品牌彩电的销售量统计图，则甲、丙两种品牌彩电该月的销售量之和为＿＿＿.
19，某省某市2005年4月1日至7日每天的降水百分率如下表：
| 日期（日） | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 降水百分率 | 30% | 10% | 10% | 40% | 30% | 10% | 40% |
则这七天降水的百分率的众数和中位数分别为＿＿＿.
20，若一个三角形的三边分别为3k，4k，5k（k为自然数），则这个三角形为＿＿＿三角形.
21，双曲线y＝
和一次函数y＝ax+b的图象的两个交点分别是A（－1，－4），B（2，m），则a+2b＝________.
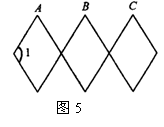
22，如图5，是根据四边形的不稳定性制作的边长均为15cm的可活动菱形衣架，若墙上钉子间的距离AB＝BC＝15cm，则∠1＝______度.
23，如图6，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点 （点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是_______.
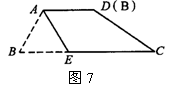
24，如图7，梯形纸片ABCD，∠B＝60°，AD∥BC，AB＝AD＝2，BC＝6，将纸片折叠，使点B与点D重合，折痕为AE，则CE＝_______.
 | |||||
 |  |
三、认真做一做，祝你成功（共52分）
25，解方程：
+
＝
.
26，先化简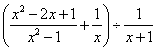
，再取一个你认为合理的x值，代入求原式的值.
27，已知反比例函数y＝的图象经过点（4，
），若一次函数y＝x+1的图象平移后经过该反比例函数图象上的点B（2，m），求平移后的一次函数图象与x轴的交点坐标.
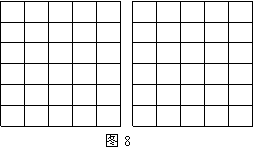
28，如图8，正方形网格中的每个小正方形边长都为1，每个小正方形的顶点叫格点，以格点为顶点分别按下列要求画三角形和平行四边形.
（1）使三角形三边长为3，2，.
（2）使平行四边形有一锐角为45°，且面积为4.
29，某校九年级学生在“五四”期间开展踢毽子比赛活动，每班派5名学生参加，按团体总分多少排列名次，在规定的时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位：个)
请你运用所学过的统计知识，加以评判；你认为应该把冠军奖状发给哪个班级？并说明理由.
| 班级 | 1号 | 2号 | 3号 | 4号 | 5号 | 6号 |
| 甲 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙 | 89 | 100 | 95 | 119 | 97 | 500 |
30，A玉米试验田是边长为a米的正方形减去边长为1米的蓄水池后余下部分；B玉米试验田是边长为(a－1)米的正方形，两块试验田的玉米都收获了500千克.
（1）哪种玉米田的单位面积产量高？
（2）高的单位面积产量是低的单位面积产量的多少倍？
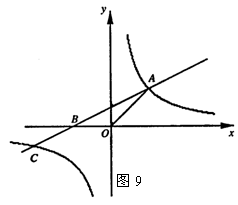
31，如图9，直线y＝kx+2k (k≠0)与x轴交于点B，与双曲线y＝(m+5)x2m+1交于点A、C，其中点A在第一象限，点C在第三象限.
（1）求双曲线的解析式；
（2）求B点的坐标；
（3）若S△AOB＝2，求A点的坐标；
（4）在（3）的条件下，在x轴上是否存在点P，使△AOP是等腰三角形？若存在，请求出P点的坐标；若不存在，请说明理由.
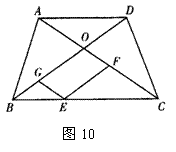
32，如图10，已知在梯形ABCD中，AD∥BC，AB＝DC，对角线AC和BD相交于点O，E是BC边上的一个动点（点E不与B、C两点重合），EF∥BD交AC于点F，EG∥AC，交BD于点G.
（1）求证：四边形EFOG的周长等于2OB；
（2）请你将上述题目的条件“梯形ABCD中，AD∥BC，AB＝DC”改为另一种四边形，其它条件不变，使得结论“四边形EFOG的周长等于2OB”仍成立，并将改编后的题目画出图形，写出已知，求证，不必证明.
 | |||
 | |||
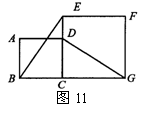33，如图11，正方形ABCD的边CD在正方形ECGF的边CE上，连接BE、DG.
（1）观察猜想BE与DG之间的大小关系，并证明你的结论；
（2）图中是否存在通过旋转能够互相重合的两个三角形？若存在，请说出旋转过程；若不存在，请说明理由.
参考答案：
一、1，B；2，C；3，D；4，B；5，A；6，C；7，B；8，A；9，B；10，C；11，A；12，B.
二、13，x+y；14，－；15，－；16，30、20；17，10或2
；18，75台；19，10%，30%；20，直角；21，－2；22，120；23，2.5；24，4.
三、25，此方程无解；
26，原式＝
. 取x＝2时， 原式＝
；
27，反比例函数的解析式为y＝
，平移后的一次函数解析式为y＝x－1，平移后的一次函数图象与x轴的交点坐标为（1，0）；
28，略；
29，（1）从平均数来看：平均数都是100，可见两班成绩相同，（2）从中位数来看：甲班是100，乙班是97，甲班好于乙班，（3）从优秀率来看：甲班60％。乙班40％，甲班好于乙班，（4）从样本方差来看：甲班是41，乙班是92，甲班的成绩比乙班稳定.综上氘核，将冠军奖状发给甲班；
30，（1）A玉米试验田面积是(a2－1)米2，单位面积产量是
千克/米2；B玉米试验田面积是(a－1)2米2，单位面积产量是
千克／米2；因为a2－1－(a－1)2＝2(a－1)，而a－1＞0，所以0＜(a－1)2＜a2－1. 所以＜.即B玉米的单位面积产量高.（2）因为÷＝×
＝
＝
.所以高的单位面积产量是低的单位面积产量的倍；
31，（1）由已知条件，得2m+1＝－1，得m＝－1，即双曲线的解析式y＝
，（2）对于y＝kx+2k，当y＝0时，x＝－2，所以B点的坐标为（－2，0），（3）设A的坐标是(x1，y1)，因为S△AOB＝2，所以y1＝2，即求得x1＝2，所以A的坐标是（2，2），（4）符合条件的P点共有4个，坐标为（2，0），（2，0），（－2，0），（4，0）；
32，（1）证四边形EFOG是平行四边形，因为四边形EFOG的周长＝2（OG+GE）＝2（OG+GB）＝2OB，（2）把等腰梯形ABCD改成矩形或正方形均可；
33，（1）BE＝DG，（2）存在，是Rt△BCE和Rt△DCG，将Rt△BCE绕点C顺时针旋转90°，可与Rt△DCG完全重合.