八年级数学第一次阶段性测试试卷
一. 精心选一选(每小题4分,共40分)
 1. 在圆的周长
1. 在圆的周长![]() 中,常量与变量分别是( )
中,常量与变量分别是( )
A. 2![]() 是常量,C、R是变量 B. 2是常量,C、
是常量,C、R是变量 B. 2是常量,C、![]() 、R是变量
、R是变量
C. C、2是常量,R是变量 D. 2是常量,C、R是变量
2.函数y=kx的图象经过点P(-1,3),则k的值为( )
A.3 B.-3 C.![]() D.-
D.-![]()
3. 下列函数关系式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 。其中一次函数的个数是( )
。其中一次函数的个数是( )
A. 1个 B.2个 C.3个 D.4个
4.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),
那么此一次函数的解析式为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若一次函数y=(3-k)x-k的图象经过第一、三、四象限,则k的取值范围是( )
A.k>3 B.0<k≤3 C.0≤k<3 D.0<k<3
6. 直线![]() ,
,![]() ,
,![]() 共同具有的特征是( )
共同具有的特征是( )
A. 经过原点
B. 与![]() 轴交于负半轴
轴交于负半轴
C. ![]() 随
随![]() 增大而增大
D.
增大而增大
D. ![]() 随
随![]() 增大而减小
增大而减小
7. 若函数y=(k-1)x+k2-1是正比例函数,则k的值为( )
A.0 B.1 C.±1 D.-1
8.已知方程ax+b=0的解是-2,下列图象肯定不是直线 y=ax+b的是( )

9.将一次函数y=2x-3的图象向右平移3个单位长度,再向上平移1个单位,平移后的直线的解析式为( )
A.y =2x - 2 B.y = 5x - 2 C.y = 2x - 8 D.y = 2x + 2
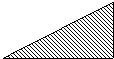 10.甲、乙二人在如图所示的斜坡AB上作往返跑训练.已知:甲上山的速度是a米/分,下山的速度是b米/分,(a<
10.甲、乙二人在如图所示的斜坡AB上作往返跑训练.已知:甲上山的速度是a米/分,下山的速度是b米/分,(a<![]() ;乙上山的速度是
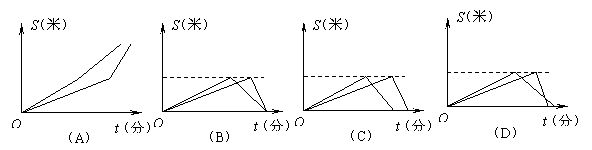
;乙上山的速度是![]() a米/分,下山的速度是2b米/分.如果甲、乙二人同时从点A出发,时间为t(分),离开点A的路程为S(米).那么下面图象中,大致表示甲、乙二人从点A出发后的时间t(分)与离开点A的路程S(米)之间的函数关系的是( )
a米/分,下山的速度是2b米/分.如果甲、乙二人同时从点A出发,时间为t(分),离开点A的路程为S(米).那么下面图象中,大致表示甲、乙二人从点A出发后的时间t(分)与离开点A的路程S(米)之间的函数关系的是( )
二.仔细填一填(每小题4分,共40分)
1. 函数![]() 中,自变量x的取值范围是________________.
中,自变量x的取值范围是________________.
2. 直线y=-2x+6与x轴的交点坐标为___________,与y轴的交点坐标为__________.图象与坐标轴所围成的三角形面积是 .
3. 若直线![]() 和直线
和直线![]() 的交点坐标为(m,8).则m= ,b= .
的交点坐标为(m,8).则m= ,b= .
4. 一次函数y=5-x与y=2x-1图象的交点为(2,3),则方程组![]() 的解为 .
的解为 .
5.已知函数y=-2x+1,若1≤y≤3时,相应的x的取值范围是________________.
6. 已知m是整数,且一次函数y=(m + 4)x + m + 2的图象不经过第二象限,则m =________.
7.当自变量x满足_________时,直线y=-x+2上的点在x轴下方.
8.在一次函数![]() 的图象上取点P,作PA⊥x轴,PB⊥y轴;垂足分别为A、B,且矩形OAPB的面积为2,则这样的点P共有_____________个。
的图象上取点P,作PA⊥x轴,PB⊥y轴;垂足分别为A、B,且矩形OAPB的面积为2,则这样的点P共有_____________个。
9. 写出同时具备下列两个条件的一次函数表达式:
(写出一个即可) .
(1) y随着x的增大而减小;
(2) 图象经过点(0,-3).
![]() 10.在计算器上按照下面的程序进行操作:
10.在计算器上按照下面的程序进行操作:
下表中的x与y分别是输入的6个数及相应的计算结果:
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -5 | -2 | 1 | 4 | 7 | 10 |
![]() 上面操作程序中所按的第三个键和第四个键 应是
.
上面操作程序中所按的第三个键和第四个键 应是
.
三.认真解一解(共70分)
1.(8分)一次函数y=kx+b的图象如图所示:
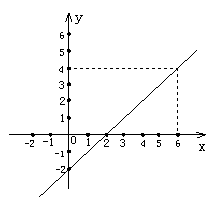 (1)求出该一次函数的关系式.
(1)求出该一次函数的关系式.
(2)当x=10时,y的值是多少?
(3)当y=12时,x的值是多少?
![]() 2. (8分) 已知:
2. (8分) 已知:![]() 与
与![]() 成正比例,且
成正比例,且![]() 时,
时,![]() 。
。
(1)
求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)
点![]() 在这个函数的图像上,求
在这个函数的图像上,求![]() 的值。
的值。
3. (12分)已知一次函数![]() ,求:
,求:
① 当![]() 为何值时,
为何值时,![]() 的值随
的值随![]() 的增加而增加;
的增加而增加;
② 当![]() 为何值时,此一次函数也是正比例函数;
为何值时,此一次函数也是正比例函数;
③ 若![]() 求函数图像与
求函数图像与![]() 轴和
轴和![]() 轴的交点坐标;
轴的交点坐标;
④
若![]() ,写出函数关系式,画出图像,根据图像求
,写出函数关系式,画出图像,根据图像求![]() 取什么值时,
取什么值时,![]() .
.
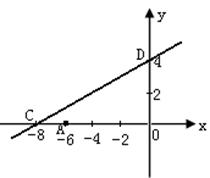
 4. (12分) 如图,直线
4. (12分) 如图,直线![]() 与x轴、y轴分别交于点C、D,点C的坐标为(-8,0),点A的坐标为(-6,0).
与x轴、y轴分别交于点C、D,点C的坐标为(-8,0),点A的坐标为(-6,0).
(1) 求k的值和该直线的函数解析式;
(2) 若点P(x,y)是第二象限内的直线上的一个动点,当点P运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3) 探究:当P运动到什么位置时,△OPA的面积为3,并说明理由.
 |
5.(8分)某人从A城出发,前往离A城30千米的B城。现在有三种车供他选择:①自行车,其速度为15千米/时;②三轮车,其速度为10千米/时;③摩托车,其速度为40千米/小时。
(1)用什么车能使他从A城到达B城的时间小于2小时,请说明理由。
(2)设此人在行进途中离A城的路程为s千米,行进时间为t小时,就(1)所选定的方案,试写出s与t的函数关系式(注明自变量t的取值范围)。并在平面直角坐标系中画出此函数的图像。
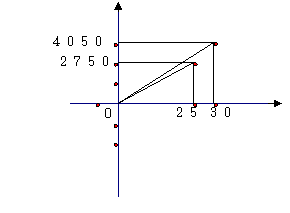
6.(12分)小R家最近购买了一套住房。准备在装修时用木质地板铺设居室。用瓷砖铺设客厅。经市场调查得知:用这两种材料铺设地面的工钱不一样,小R根据地面的面积,对铺设居室和客厅的费用(购买材料费和工钱)分别做了预算,通过列表,并用x(m2)表示铺设地面的面积,用y(元)表示铺设费用,制成如图所示,请你根据图中所提供的信息,解答下列问题
(1)预算中铺设居室的费用为____元/m²,铺设客厅的费用为___元/m²;
(2)表示铺设居室的费用y元与面积x(m²)之间的函数关系式为______。表示铺设客厅的费用y(元)与面积x(m²)之间的关系式为________。
(3)已知在小R的预算中。铺设1m²的瓷砖比铺设木质地板的工钱多5元;购买1m²的瓷砖是购买1m²木质地板费用的3/4。那么,铺设每平方米木质地板、瓷砖的工钱各是多少元?购买每平方米的木质地板、瓷砖的费用各是多少元?
 居室
居室
客厅
7.(10分)阅读:我们知道,在数轴x=1表示一个点,而在平面直角坐标系中x=1表示一条直线;我们还知道,以二元一次方程2 x – y + 1 = 0的所有解为坐标的点组成的图形就是一次函数y = 2 x - 1的图象,它也是一条直线如图①。
![]() 观察图①可以解出,直线x=1现直线y = 2 x -1的交点P的坐标(1,3),就是方程组
观察图①可以解出,直线x=1现直线y = 2 x -1的交点P的坐标(1,3),就是方程组![]() 的解,所以这个方程组的解为
的解,所以这个方程组的解为 ![]()
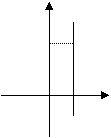
 在直角坐标系中,x≤1表示一个平面区域,即直线x = 1以及它左侧的部分,如图②;y≤2
x + 1也表示一个平面区域,即直线y = 2 x+1以及它下方的部分,如图③。
在直角坐标系中,x≤1表示一个平面区域,即直线x = 1以及它左侧的部分,如图②;y≤2
x + 1也表示一个平面区域,即直线y = 2 x+1以及它下方的部分,如图③。
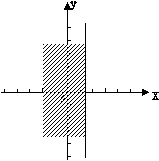

(1,3)
O 1 x 1
(图①) (图②) (图③)
回答下列问题:
(1)在直角坐标系(图④)中,用作图象的方法求出方程组![]() 的解;
的解;
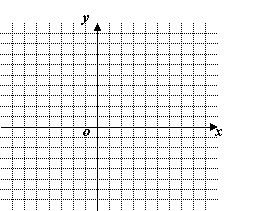 (2)用阴影表示
(2)用阴影表示 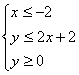 所围成的区域。
所围成的区域。