八年级数学第一学期第二次阶段检测
命题人: 孙加其 张晓宏 （时间：100分钟 总分：100分）
一、选择题（本题共10小题；每小题3分，共30分）
下列各题都有代号为A、B、C、D的四个结论供选择，其中只有一个结论是正确的．请把正确选项的代号填入下列表格内。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 选项 |
1．下列平面图形中，不是轴对称图形的是 （ ）
2．关于函数
,下列结论正确的是
( )
A． 图象必经过
B． 当
时，
C． 图象经过第一、二、三象限
D． 
随
的增大而增大
3．一个样本中有80个数据，其中最大值是141，最小值是50，取组距为10，则这个样本可以分成 （ ）
A．10组 B．9组 C．8组 D．7组
4．下列计算中，错误的是 ( )
A．
B．
C．
D．
5．关于x的多项式
与
相加后，不含
项，则
等于 （ ）
A． 2 B． -2 C． -4 D． -8
6．已知：在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于D，若BC=32，且BD：DC=9：7，则D到AB边的距离为 （ ）
A．18 B．16 C．14 D．12
7．若三点
在一条直线上，则
的值为
（ ）
A． 2 B． 3 C．-7 D．0
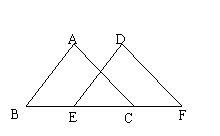
8．已知：如图，△ABC与△DEF是全等三角形，则图中相等的线段的组数是 （ ）
A．3 B． 4
C．5
D．6
（第8题） （第9题） （第10题）
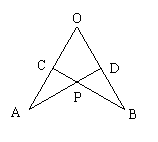
9．如图，在∠AOB的两边上截取AO=BO，CO=DO，连接AD，BC交于点P，那么在结论
①△AOD≌△BOC ；②△APC≌△BPD；③点P在∠AOB的平分线上．其中正确的是 （ ）
A．只有① B． 只有② C． 只有①② D． ①②③
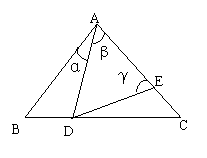
10．如图，D，E分别是△ABC的边BC，AC，上的点，若AB=AC，AD=AE，则 （ ）
A．当∠B为定值时，∠CDE为定值 B．当∠α为定值时，∠CDE为定值
C．当∠β为定值时，∠CDE为定值 D．当∠γ为定值时，∠CDE为定值
二、填空题（本题共10小题；每小题2分，共20分）
请把最后结果填在题中横线上．
11．函数
中,自变量的取值范围是 ．
12．在某次考试中全班50人中有10人获得优秀等级，那么绘制扇形图描述成绩时，优秀等级所在的扇形的圆心角是____________度．
13．已知
与
的和是单项式，则
，
．
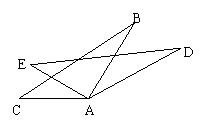
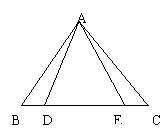14．如图，△ABC≌△ADE，∠EAC=25°，则∠BAD= °
| ||||
| ||||
|
16．把点A (a,3)向上平移三个单位正好在直线y＝－x＋1上，则a的值是 ．
17．已知
那么
．
18．等腰三角形一腰上的高与另一腰的夹角为40°，则它的顶角的度数为 °．
|
| ||||
| ||||
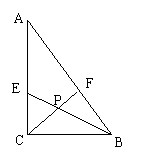
20．如图，在△ABC中，∠ACB=90°，BE平分∠ABC，CF平分∠ACB，CF,BE交于点P，AC=4
，BC=3，AB=5，则△CPB的面积为
三、解答题（本大题共50分）
21．①（本题4分）计算： 
② （本题4分）化简求值：
其中
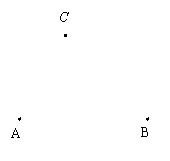22．（本题4分）如图,A、B、C三点表示3个村庄，为了解决村民子女就近入学问题，计划新建一所小学，要使学校到3个村庄的距离相等，请你在图中有尺规确定学校的位置．(保留作图痕迹,写出画法)
画法:
23．（本题6分）已知直线
与直线
交于点
，求
的值，及两直线与两坐标轴所围成的四边形的面积．
24． (本题6分) 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,
求△ABC各角的度数.
25．(本题6分)初三某班对最近的一次数学考试成绩（得分取整数）进行统计分析，将所有成绩由低到高分成5组，并绘制成如图所示的频数分布直方图，请结合直方图提供的信息，回答下列问题：
（1）该班共有___________名同学参加这次考试;
（2）在该频数分布直方图中画出频数折线图；
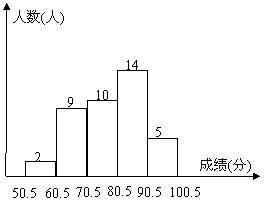（3）若这次考试中，成绩80分以上（不含80分）为优秀，那么该班这次数学考试的优秀率是多少？
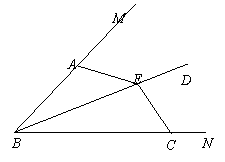26．（本题5分）如图,BD平分∠MBN,A，C分别为BM,BN上的点,且BC>BA,E为BD上的一点,AE=CE,求证 ∠BAE+∠BCE=180°
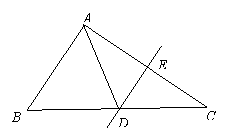
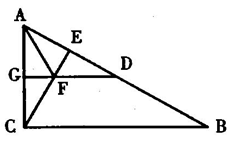
27（本题7分）如图，在△ABC中，∠ACB=90°，CE⊥AB于点E，AD=AC，AF平分∠CAB交CE于点F，DF的延长线交AC于点G，
求证：（1）DF∥BC；（2）FG=FE．
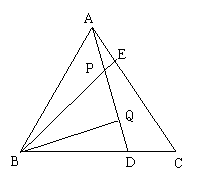28．（本题8分） 如图, △ABC为等边三角形,AE=CD,AD、BE相交于点P，BQ⊥AD与Q，PQ=4，PE=1
(1)求证 ∠BPQ=60°
(2)求AD的长