八年级数学第一学期第三次月考
八 年 级 试 卷
（时间：100分钟 总分：100分）
一、选择题
1．下列计算正确的是( )
A．a·a2＝a2 B．(a2)2＝a4 C．a2·a3＝a6 D．(a2b)3＝a2·b3
2. 下列给出的四个点中，不在直线y =2x-3上的是（ ）
A.（1， -1） B.（0， -3） C.（2， 1） D.（-1，5）
3．下列各式成立的是（ ）
A．a-b+c=a-（b+c） B．a+b-c=a-（b-c）
C．a-b-c=a-（b+c） D．a-b+c-d=（a+c）-（b-d）
4. 下列函数中，图象一定经过原点的是（ ）
A．
B.
C.
D.
5．下列式子中，从左到右的变形是因式分解的是( )．
A．(x－1)(x－2)＝x2－3x＋2 B．x2－3x＋2＝(x－1)(x－2)
C．x2＋4x＋4＝x(x一4)＋4 D．x2＋y2＝(x＋y)(x—y)
6.下列多项式： ①
②
③
④
，
其中能用完全平方公式分解因式的有 ( )
A．1个 B．2个 C．3个 D．4个
7．下列命题错误的是（ ）
A、全等三角形的对应边上的高相等；
B、全等三角形的面积相等；
C、一个锐角和相邻的直角边对应相等的两个直角三角形全等；
D、两角对应相等的两个三角形全等.
8．如图所示，在下列条件中，不能作为判断△ABD≌△BAC的条件是； ( )
A. ∠D＝∠C，∠BAD＝∠ABC B．∠BAD＝∠ABC，∠ABD＝∠BAC
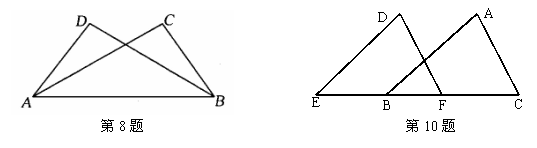C．BD＝AC，∠BAD＝∠ABC D．AD＝BC，BD＝AC
9. 下列图中，能近似描述匀速行驶的火车速度与时间的关系的是：（ ）
 |  |  |  |
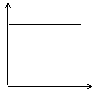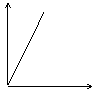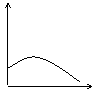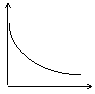(A) (B) (C) (D)
10. 如图，E、B、F、C四点在一条直线上，EB=CF，∠A=∠D，再添一个条件仍不能证明△ABC≌△DEF的是( )
A.AB=DE B. DF∥AC C. ∠E=∠ABC D. AB∥DE
二、填空题：
11．函数
中，自变量的取值范围是____________。
12．把
这个函数的图象向下平移一个单位长度后，所得的直线解析式
是_____________________。
13 在函数y=(k-1)x中，y随x增大而减小，则k的范围是______________。
14．若9x2－kxy＋4y2是一个完全平方式，则k的值是_______。
15．计算(－3a3)2· (－2a2)3＝_____________
16．已知a2+b2=13，ab=6，则a+b的值是________．
17．如果△ABC≌△DEF，△DEF周长是32cm，DE=9cm,EF=13cm.∠E=∠B，则AC=________。
18．如图，某人把一块三角形的玻璃打碎成了三块，现在你要到玻璃店去配一块完全一样的玻璃，
则应带哪块玻璃去__________（填上玻璃序号）。
19．已知△ABC中，∠BAC=60°，将△ABC绕着点A顺时针旋转40°，如图所示，则
△BAC′的度数为______。
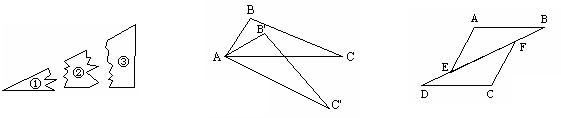
(第18题) (第19题) (第20题)
20．如图，点D、E、F、B在同一直线上，AB∥CD、AE∥CF，且AE=CF，若BD=10，BF=2，
则EF=____________。
三、解答题
21．计算
（1）
（2） 2(m＋1)2－(2m＋1)(2m—1)
22．因式分解
（1） 
（2） (a2+4b2)2－16a2b2
 |
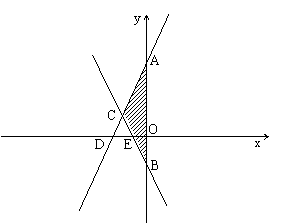24．.已知，直线y=2x+3与直线y=-2x-1.
(1)求两直线与y轴交点A、B的坐标；
(2)求两直线与x轴交点D、E的坐标；
(3)求两直线交点C的坐标；
(4)求△ABC的面积.
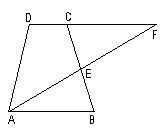25．已知：在梯形ABCD中，AB//CD，E是BC的中点，直线AE与DC的延长线交于点F。
求证：△ABE≌△FCE
26．已知：如图，AB＝AE，BC＝ED，AF⊥CD且F是CD的中点，求证：∠B＝∠E．
 |
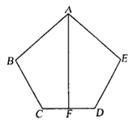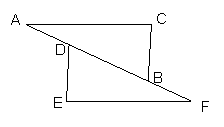
27．已知AC=FE，BC=DE，点A、D、B、F在一条直线上，要使△ABC≌△FDE，应增加什么条件？
并根据你所增加的条件证明： △ABC≌△FDE。
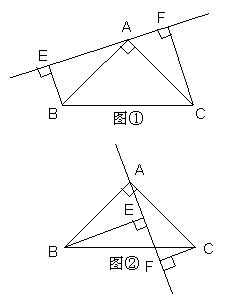
28．如图，已知△ABC中，AB=AC，∠BAC=90°，分别过B、C向过A的直线作垂线，垂足分别
为E、F。
（1）如图①过A的直线与斜边BC不相交时，求证：EF=BE+CF
（2）如图②过A的直线与斜边BC相交时，其他条件不变，若BE=10，CF=3，求：FE长。
 |