八年级数学第一学期第四次月考试卷
班级___________ 姓名___________ 学号_____________
| 题 号 | 一 | 二 | 三 | 总 分 |
| 得 分 |
|
|
|
|
温馨提示：请仔细审题，细心答题，相信你一定会有出色的表现！
一、选择题（本题有12小题，每小题3分，共36分．每小题有且只有一个选项是正确的，不选、多选、错选均不给分）
1．下列计算正确的是( )
A．a·a2＝a2 B．(a2)2＝a4 C．a2·a3＝a6 D．(a2b)3＝a2·b3
2．下列各式成立的是（ ）
A．a-b+c=a-（b+c） B．a+b-c=a-（b-c）
C．a-b-c=a-（b+c） D．a-b+c-d=（a+c）-（b-d）
3．直线y=kx+2过点（-1，0），则k的值是（ ）
A．2 B．-2 C．-1 D．1
4．和三角形三个顶点的距离相等的点是（ ）
A．三条角平分线的交点 B．三边中线的交点
C．三边上高所在直线的交点 D．三边的垂直平分线的交点
5．下列说法中，正确的个数为 ( )
①扇形统计图是用圆代表总体，圆中的各个扇形分别代表总体中的不同部分 ②要清楚的表示出各部分在总体中所占的百分比应选择条形统计图 ③要反映某日气温的变化情况，应选择折线统计图
A. 0个 B．1个 C. 2个 D．3个
6．等腰三角形一边长等于4，一边长等于9，它的周长是 ( )
A．17 B．22 C．17或22 D．13
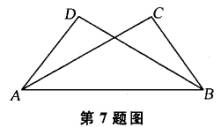
7．如图所示，在下列条件中，不能作为判断△ABD≌△BAC的条件是 ( )
A. ∠D＝∠C，∠BAD＝∠ABC B．∠BAD＝∠ABC，∠ABD＝∠BAC
C．BD＝AC，∠BAD＝∠ABC D．AD＝BC，BD＝AC
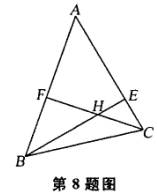
8．如图，已知BE，CF分别为△ABC的两条高，BE和CF相交于点H，若∠BAC＝50°，则∠BHC为 ( )
A．160° B．150° C．140° D．130°
9．使两个直角三角形全等的条件是 ( )
A. 斜边相等;B．两直角边对应相等; C．一锐角对应相等;D．两锐角对应相等
10．在边长为a的正方形中挖掉一个边长为b的小正方形(a>b)，把余下的部分剪拼成一个矩形(如图)．通过计算图形(阴影部分)的面积，验证了一个等式，则这个等式是( )
A．a2一b2＝(a＋b)(a—b) B．(a＋b)2＝a2＋2ab＋b2
C．(a—b)2＝a2－2ab＋b2 D．a2－ab＝a(a—b)
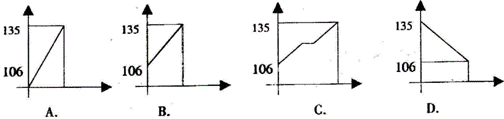
11.三峡工程在6月1日与6月10日下闸蓄水期间，水库水位由106米升至135米，高峡平湖初现人间，假设水库水位匀速上升，那么下列图象中，能正确反映这10天水位h（米）随时间t（天）变化的是
（ ）
12．如图中的图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中，汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系，根据图中提供的信息，给出下列说法：①汽车共行驶了120千米；②汽车在行驶途中停留了0.5小时；③汽车在整个行驶过程中的平均速度为 千米／时；④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少．其中正确的说法共有( )
A.1个 B．2个 C．3个 D．4个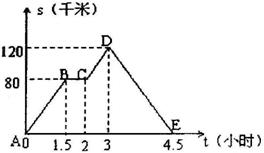
二、填空题（本题有12小题,每小题3分,共33分）
13. 单项式－ab2 的系数是 。
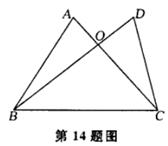
14．如图，已知∠ACB＝∠DBC，要使△ABC≌△DCB，只需增加一个条件是______．
15.在平面镜里看到背后墙上的电子钟示数，是20：15，这时的实际时间应该是_________．
16．已知△ABC≌△DEF，若∠A=60°，∠F=90°，DE=6cm，则AC=________．
17．点P关于x轴对称的点是（3，-4），则点P关于y轴对称的点的坐标是_______．
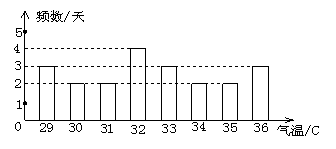
18．根据某市去年7月份中某21天的各天最高气温（℃）记录，制作了如图所示的统计图，由图中信息可知，最高气温达到35℃（包括35℃）以上的天数有________天．
19．今天数学课上，老师讲了多项式的加减，放学后，小明回到家拿出课堂笔记，认真的复习老师课上讲的内容，他突然发现一道题：(—x2＋3xy－y2)－(－x2＋4xy－y2)＝－x2______________________＋y2空格的地方被钢笔水弄污了，请你帮他补上!
20．填空：x2＋( )＋＝( )2；( )(－2x＋3y)＝9y2—4x213．在扇形统计图中，有两个扇形的圆心角度数之比为3∶4，且知较小扇形表示24本课外书，那么较大扇形表示_______本课外书．
21．若等腰三角形的顶角为100°，则它腰上的高与底边的夹角是_______。
22．若y＋6与x＋a(a，b是常数)成正比例，且当x＝3时，y＝5，当x＝2时，y＝2，则y与x的函数关系是_______
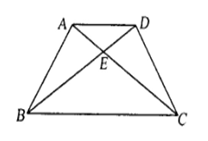23．如右图，∠BAC＝∠CDB＝90°，BE＝EC，则图中的全等 角形有_______对，
三、解答题(共81分)
24．(每题4分，共12分)
（1）(m＋1)2－(2m＋1)(2m—1)
(2)4x2－(2－x＋3)(－2x－3).
（3）（a+b）(a－b)(a
－b)
25．（5分）先化简再求值：[（x+2y）（x-2y）-（x+4y）2]÷（4y），其中x=5，y=2．
26．（5分）解方程：（2x+3）(2x-3)=(2x+3)
27．（9分）用简便方法计算：
（1）30
×29
(2) 99－98×100
(3)2005
28．（10分）已知图7中A、B分别表示正方形网格上的两个轴对称图形（阴影部分），其面积分别记为S1、S2（网格中最小的正方形的面积为一个单位面积），请你观察并回答问题．
（1）填空：S1：S2的值是__________．
（2）请你在图C中的网格上画一个面积为8个平方单位的轴对称图形．
29．(10分)为了保护学生的视力，课桌的高度)ycm与椅子的高度xcm(不含靠背)都是按y是x的一次函数关系配套设计的，下表列出了两套课桌椅的高度：
(1)请确定)y与x的函数关系式(不要求写出x的取值范围)；
(2)现有一把高42.0cm的椅子和一张高78.2cm的课桌，它们是否配套?请通过计算说明理由。
| 第一套 | 第二套 | |
| 椅子高度xcm | 40.0 | 37.0 |
| 课桌高度ycm | 75.0 | 70.2 |
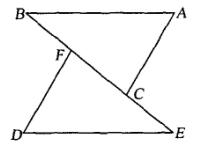
30．(5分)已知，如图，点B、F、C、E在同一直线上，FB＝CE，AB∥ED，AC∥FD．
求证：AB＝ED，AC＝DF．
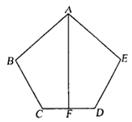31．（5分）已知：如图，AB＝AE，BC＝ED，AF是CD的垂直平分线，
求证：∠B＝∠E．
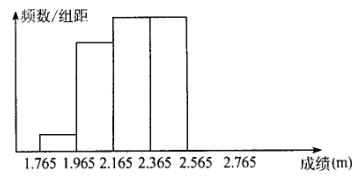
32．(10分)某校500名男生参加体育中考立定跳远测试，将所得成绩整理后分成五组，画出部分频率分布直方图，已知图中从左到右前四个小组的频率依次是0.04,0.24，0.28，0.28．
(1)求第五小组的频率，并补全频率分布直方图；
(2)若规定2.165m以上为满分，试问该校男生立定跳远得满分的人数有多少?
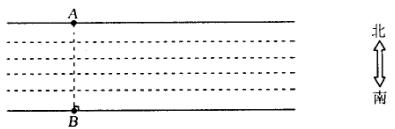
33．（10分）一条大河两岸的A、B处分别立着高压线铁塔，如图所示．假设河的两岸平行，你在河的南岸，请利用现有的自然条件、皮尺和标杆，并结合你学过的全等三角形的知识，设计一个不过河便能测量河的宽度的好办法．(要求，画出示意图，并标出字母，结合图形简要叙述你的方案)
