八年级数学第一学期教学案
3．5 矩形、菱形、正方形（2）
学习目标：1、 熟练掌握矩形判定，并且能够熟练的运用；
2、 通过自主探索、合作交流矩形的判定，发展学生的探究意识和有条理的表达能力；
学习重点：矩形的判定和灵活运用
学习难点: 矩形的判定和灵活运用
学习过程：
一、复习提问
1、什么样的四边形叫矩形？
2、矩形有哪些性质？
二、创设情境
某木工做了一个矩形门框运到学校工地上安装，在到达工地时，检查人员怀疑在运送过程中有变形，请你帮助检查人员想一个方法来检验这个木门是否变形？
三、新课讲解
师生共同探究矩形的识别方法：
1、 的平行四边形是矩形
2、 的四边形是矩形
讨论：检验门框的方法共有几种？
四、课堂练习：
1、 填空：
有一个角是 的平行四边形是矩形；有＿＿＿个角是＿＿＿＿角的四边形是矩形；对角线相等的＿＿＿＿是矩形；对角线＿＿＿＿＿＿＿＿的四边形是矩形.
2、 判断（正确的打√，错误的打×）
⑴有一个角是直角的四边形是矩形。 （ ）
⑵对角线相等的四边形是矩形。 （ ）
⑶对角线相等且互相平分的四边形是矩形 （ ）
⑷四个角相等的四边形是矩形 （ ）
⑸对角互补的平行四边形是矩形 （ ）
⑹对角线互相平分且有一组对角互补的四边形是矩形 （ ）
⑺对角线相等且有一个角是直角的四边形是矩形 （ ）
⑻有一组对边平行，有两个角是直角的四边形是矩形 （ ）
五、例题讲解
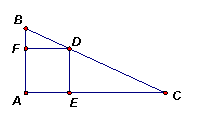
例1、在直角△ABC中，∠A=90°，D为BC上一点，DE∥AB交AC于E点，DF∥AC交AB于F点，试判别四边形AEDF的形状，并说明理由。
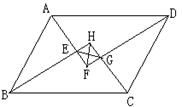
例2、已知：在平行四边形ABCD中，各个内角的平分线分别相交于点E、F、G、H。
⑴猜想：EG与FG间的关系是 ；
⑵试说明你的猜想的正确性。
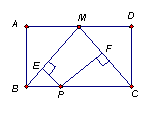
例3、点M是矩形ABCD的边AD的中点，P为BC上的一点，且PE⊥MC，PF⊥MB，当AB、AD满足什么条件时，四边形PEMF是矩形。
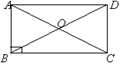
例4、如图示，四边形ABCD的对角线ACBD相交于点O，OA=OC，OB=OD且AC=BD，请你说明四边形ABCD是矩形
 |
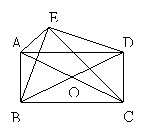例5、如图，平行四边形ABCD中，以AC为斜边作Rt△ACE，又∠BED=90°，求证：四边形ABCD是矩形
六、课堂小结：矩形的判定方法是什么？
七、作业：P100 1（1）（2）、4、5
主备人：俞永亮 审核人：夏存才