八年级数学第一学期教学案
3.5矩形、菱形、正方形 第１课时
教学目标 1、理解矩形的概念，掌握矩形的性质；
2、引导学生经历由平行四边形到矩形的探索过程，在活动中发展学生的探究意识，合情推理能力有条理地表达的能力；
3、在对矩形特殊性质探索过程中，引导学生理解特殊与一般的关系，领会特殊事物的本质属性与其特殊性质的关系.
教学重点：探索矩形的性质及其性质的简单运用.
教学难点：矩形与平行四边形之间的内在联系与区别.
教学过程
一、 学前准备
1．在平行四边形ABCD中写出尽可能多的结论（边、角、对角线之间的关系）
（1） （2） （3）
（4） （5） （6）
（7） （8）
2．平行四边形是中心对称图形，其对称中心是
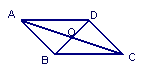
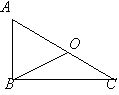3．如图，BO是Rt△ABC的斜边AC的中线.
（1）画出△ABC关于点O对称的图形
（2）把点B关于点D对称点记为D，连结DA、DC，
想一想四边形ABCD是中心对称图形吗？说说你的理由.
（3）四边形ABCD有什么特点？请说说你的想法及理由
二、 自学、合作探究
1． 叫做矩形 （通常也叫长方形）
2．矩形是特殊的平行四边形，它具有 的一切性质。你能说出这些性质吗？
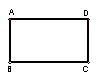3．在矩形ABCD中，如果∠A=90°，请你求∠B，∠C，∠D的度数并说明理由
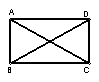4．在矩形ABCD中，连结对角线AC，BD
（1） 测量AC，BD的长度，你发现：
（2） 你能用学过的知识说明你的发现是正确的吗？
5．由3和4两小题你能发现：矩形除具有一般平行四边形的一切性质外，还具有一些特殊（一般平行四边形没有）的性质，请你把它写出来好吗？
。
6．利用矩形的性质解答下列问题
（1）矩形的面积为48，一条边长为6，则矩形的另一边长为 ，对角线为
（2）矩形的一条对角线长为10，则另一条对角线长为 ，如果一边长为8，则矩形的面积为
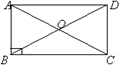7（课本P118例1）如图矩形ABCD的对称线相交于点O，AB＝4cm，∠AOB＝60°（1）求对角线AC的长.（2）求矩形ABCD的周长
三、应用与探究
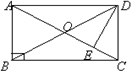1．如图，在矩形ABCD中，DE⊥AC，E为垂足，∠EDA：∠EDC＝3：1.求∠BDE的度数.
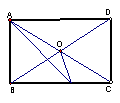2．如图，矩形ABCD中，AE平分∠BAD，交BC于E，对角线AC、BD交于O，若∠OAE＝15°
（1） 说明：OB＝BE（2）求∠BOE的度数
3、矩形是具有而平行四边形不一定具有的性质是＿＿＿＿（填代号）
①对边平行且相等；②对角线互相平分；③对角相等
④对角线相等； ⑤4个角都是90°； ⑥轴对称图形
4、矩形是轴对称图形，对称轴是＿＿＿＿＿又是中心对称图形，对称中心是＿＿＿
5、矩形两对角线把矩形分成＿＿＿个等腰三角形
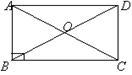6．如图，矩形ABCD中，对角线相交于点O，AC＝8cm，∠AOB＝60°，求此矩形的边长.
课堂练习P93 1，2，3
课堂作业P100 2,3
主备人翁增广 审核人 夏存才