八年级数学（上）第二章提高练习
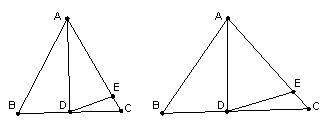
1．如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD，
（1）求证：△BCE≌△DCF; （2）若AB=21，AD=9，BC=CD=10，求AC的长。
 |
2．如图，要为一段高为5米，长为13米的楼梯铺上红地毯，则红地毯至少要 米长；
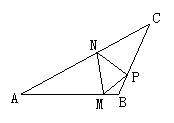
3．如图所示，△ABC中，∠ABC=100°，AM=AN，CN=CP，求∠MNP的度数．
4．如果一个角的两边与另一个角的两边分别平行，则这两个角的关系是( )
A、相等 B、互余 C、互补 D、相等或互补
5．若一个三角形的两个角的平分线分别垂直对边，则这个三角形是
A、等边三角形 B、等腰三角形 C、等腰直角三角形 D、直角三角形
6．已知：a、b、c是△ABC的三边，且满足（a-b）（a2+b2-c2）=0，则△ABC是( )
A、等腰三角形 B、直角三角形
C、等腰三角形或直角三角形 D、等腰直角三角形
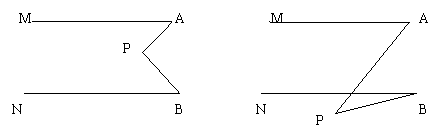
7．已知，如图，直线MA∥NB，
（1）若点P在直线MA与NB之间，你能得到∠APB=∠MAP+∠NBP这个结论吗？并说明你的理由。
（2）又若点P在两条直线MA与NB之外时，又会有什么结论？你还能就本题作出什么新的猜想。
8．已知等腰直角三角形的面积为16cm2，那么斜边上的高为（ ）.
A.4cm B.8cm C.4cm和8cm D.2cm
9．如图（1），等边
中，D是AB边上的动点，以CD为一边，向上作等边
，连结AE。
1）
和
会全等吗？请说说你的理由。
2）试说明AE∥BC的理由
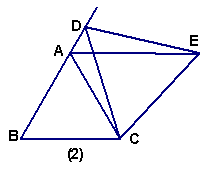3）如图（2），将（1）中点D运动到边BA的延长线上，所作仍为等边三角形。请问是否仍有AE∥BC？证明你的猜想。
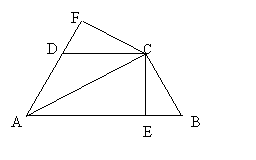
10．如图:在△ABC中，E是BC边上的一点，EF垂直BC交BA于D，交CA的延长线于F，若AD=AF.则△ABC是不是等腰三角形？请说明理由.
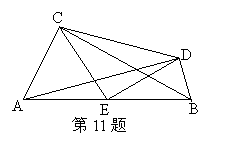
11．如图AC⊥BC，AD⊥BD，E为AB中点，连结CD，CE，DE，猜想△CDE是什么三角形？试说明理由.
 | |||
 | |||
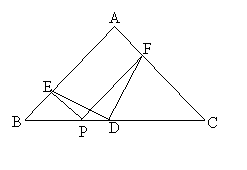
12．如图：已知点D是等腰直角三角形ABC斜边BC的中点，在BC上任意取一点P，分别作PE⊥AB于点E，PF⊥AC于点F，连接DE、DF，试说明①DE⊥DF. ②S四边形AEDF=
S△ABC的理由.
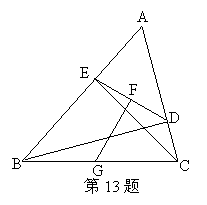13．如图:在△ABC中，已知BD，CE分别是△ABC的AC，AB边上的高，F是DE的中点，G是BC的中点.请说明GF⊥DE的理由.
 |
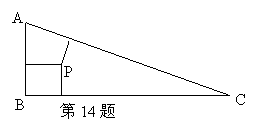14．如图:在△ABC中，∠B=90°，两直角边AB=5，BC=12，三角形内有一点P到各边的距离相等，求点P到各边的距离.
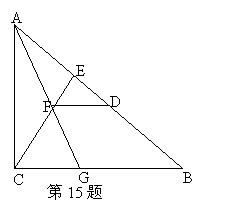15．如图:在△ABC中，∠ACB=90°，CE⊥AB于E，D是AB是一点，且AD=AC，AF平分∠CAB交CE于F，交BC于G
（1）说明CG=CF
（2）说明DF∥BC
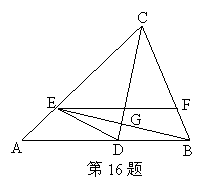
16．如图:在△ABC中，CD是∠ACB的平分线，BE⊥CD于G交AC于E，EF∥AB交BC于F，连结ED，判断BE是否平分∠DEF，并说明理由.
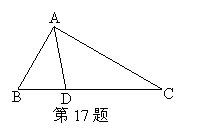17.如图，AD是△ABC中∠BAC的平分线，∠B=2∠C，你能用轴对称的性质与等腰三角形的有关知识研究线段AC与AB，BD的数量关系吗？
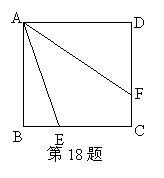
18．如图:已知正方形ABCD中，点E、F分别是BC、CD上，且AF平分∠DAE，则AE＝BE＋DF，请说明理由.
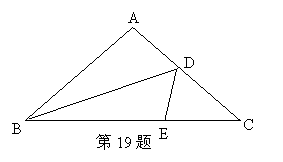19．如图:在△ABC中，AB=AC，∠A=100°，将图形沿BD对折恰使点A落在BC边上的E点，猜想BC与BD+AD的关系，并说明理由.
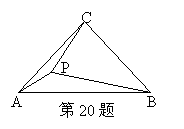
20．如图:在△ABC中，∠ACB=Rt∠，AC=BC，P是△ABC内一点且PA=1 PB=3 PC=2，你能求出∠APC的度数吗？
请试一试.
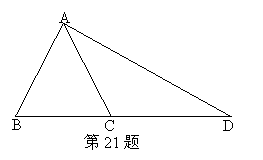
21．如图:在△ABC中，AB=AC，D是BC延长线的一点，连结AD，∠BAD=900则AD2-AB2=BD·DC请说明理由
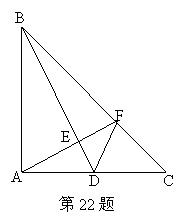22．如图:已知D是等腰直角△ABC直角边AC上的中点,AE⊥BD于E,交BC于F,则∠ADB=∠CDF,请说明理由.
23、在ΔABC中，AB=AC（1）如图1，如果∠BAD=30°，AD是BC上的高，AD=AE，则∠EDC=__________
（2）如图2，如果∠BAD=40°，AD是BC上的高，AD=AE，则∠EDC=__________
（3）思考：通过以上两题，你发现∠BAD与∠EDC之间有什么关系？请用式子表示：____________________
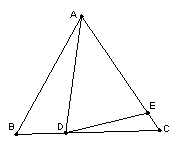（4）如图3，如果AD不是BC上的高，AD=AE，是否仍有上述关系？如有，请你写出来，并说明理由。
