八年级第三阶段考试
数 学 试 题
一、选择题（本大题共10个小题；每小题2分，共20分.在每小题给出的四个选项中，只有一项是符合题目要求的）
1、下列各式成立的是（ ）
A．a-b+c=a-（b+c） B．a+b-c=a-（b-c）
C．a-b-c=a-（b+c） D．a-b+c-d=（a+c）-（b-d）
2、直线y=kx+2过点（-1，0），则k的值是（ ）
A．2 B．-2 C．-1 D．1
3、和三角形三个顶点的距离相等的点是（ ）
A．三条角平分线的交点 B．三边中线的交点
C．三边上高所在直线的交点 D．三边的垂直平分线的交点
4、一个三角形任意一边上的高都是这边上的中线，则对这个三角形的形状最准确的判断是（ ）
A．等腰三角形 B．直角三角形
C．正三角形 D．等腰直角三角形
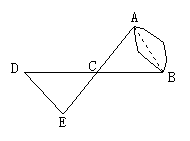
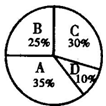
5、图1所示的扇形图是对某班学生知道父母生日情况的调查，A表示只知道父亲生日，B表示只知道母亲生日，C表示知道父母两人的生日，D表示都不知道．若该班有40名学生，则知道母亲生日的人数有（ ）
A．25% B．10 C．22 D．12
(1) (2) (3)
6、下列式子一定成立的是（ ）
A．x2+x3=x5; B．（-a）2·（-a3）=-a5 C．a0=1 D．（-m3）2=m5
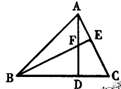
7、如图2，△ABC中，AD⊥BC于D，BE⊥AC于E，AD与EF交于F，若BF=AC，那么∠ABC等于（ ）
A．45° B．48° C．50° D．60°
8、已知x2+kxy+64y2是一个完全式，则k的值是（ ）
A．8 B．±8 C．16 D．±16
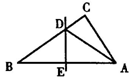
9、如图3，△ABC中边AB的垂直平分线分别交BC、AB于点D、E，AE=3cm，△ADC的周长为9cm，则△ABC的周长是（ ）
A．10cm B．12cm C．15cm D．17cm
10、已知（x+a）（x+b）=x2-13x+36，则a+b的值分别是（ ）
A．13 B．-13 C．36 D．-36
二、填空题（本大题共5个小题；每小题3分，共15分.把答案写在题中横线上）
11、点P关于x轴对称的点是（3，-4），则点P关于y轴对称的点的坐标是_______．
12、已知a2+b2=13，ab=6，则a+b的值是________．
13、直线y=ax+2和直线y=bx-3交于x轴同一点，则a与b的比值是________．
14、如图为杨辉三角表，它可以帮助我们按规律写出（a+b）n（其中n为正整数）展开式的系数，请仔细观察表中规律，填出（a+b）4的展开式中所缺的系数．
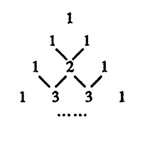（a+b）1=a+b；
（a+b）2=a2+2ab+b2；
（a+b）3=a3+3a2b+3ab2+b3；
（a+b）4=a4+_____a3b+_____a2b2+______ab3+b4
15、已知△ABC≌△DEF，若∠A=60°，∠F=90°，DE=6cm，则AC=________．
三、解答题（本大题共10个小题；共80分）
试试基本功
16、（本小题满分7分）
先化简，再求值：2x(3x2－4x＋1)－3x2(2x－3)，其中x＝－3．
17、（本小题满分7分）
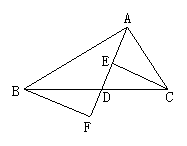
如图，AD是△ABC的中线，CE⊥AD于E，BF⊥AD交AD的延长线于F，求证：CE=BF。
归纳与猜想
18、（本小题满分7分）
下列是三种化合物的结构式及分子式，
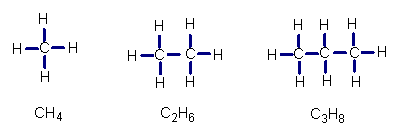
结构式
分子式
（1）请按其规律，写出后一种化合物的分子式 ．
（2）每一种化合物的分子式中H的个数m是否是C的个数n的函数？如果使写出关系式。
19、（本小题满分8分）
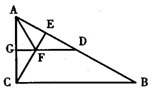
如图，在△ABC中，∠ACB=90°，CE⊥AB于点E，AD=AC，AF平分∠CAB交CE于点F，DF的延长线交AC于点G，求证：（1）DF∥BC；（2）FG=FE.
判断与决策
20、（本小题满分8分）
某批发商欲将一批海产品由A地运往B地，汽车货运公司和铁路货运公司均开办了海产品运输业务．已知运输路程为120千米，汽车和火车的速度分别为60千米/时和100千米/时．两货物公司的收费项目和收费标准如下表所示：
| 运输工具 | 运输费单价 （元/吨·千米） | 冷藏费单价 （元/吨·小时） | 过路费 （元） | 装卸及管理费 （元） |
| 汽车 | 2 | 5 | 200 | 0 |
| 火车 | 1.8 | 5 | 0 | 1600 |
注：“元/吨·千米”表示每吨货物每千米的运费；“元/吨小时”表示每吨货物每小时的冷藏费．
（1）设该批发商待运的海产品有x（吨），汽车货运公司和铁路货运公司所要收取的费用分别为y1（元）和y2（元），试求出y1和y2和与x的函数关系式；
（2）若该批发商待运的海产品不少于30吨，为节省运费，他应该选择哪个货运公司承担运输业务？
21、（本小题满分8分）
为了保护学生的视力，课桌的高度)ycm与椅子的高度xcm(不含靠背)都是按y是x的一次函数关系配套设计的，下表列出了两套课桌椅的高度：
(1)请确定)y与x的函数关系式(不要求写出x的取值范围)；
(2)现有一把高42.0cm的椅子和一张高78.2cm的课桌，它们是否配套?请通过计算说明理由。
| 第一套 | 第二套 | |
| 椅子高度xcm | 40.0 | 37.0 |
| 课桌高度ycm | 75.0 | 70.2 |
操作与探究
22、（本小题满分8分）
已知图7中A、B分别表示正方形网格上的两个轴对称图形（阴影部分），其面积分别记为S1、S2（网格中最小的正方形的面积为一个单位面积），请你观察并回答问题．
（1）填空：S1：S2的值是__________．
（2）请你在图C中的网格上画一个面积为8个平方单位的轴对称图形．
实验与推理
23、（本小题满分8分）
如图，在△ABC中，点Ｄ在AB上，点Ｅ在ＢＣ上，BD＝BE。
（１）请你再添加一个条件，使得△ＢＥＡ≌△ＢＤＣ，并给出证明。
你添加的条件是：___________
（2）根据你添加的条件，再写出图中的一对全等三角形：____________（只要求写出一对全等三角形，不再添加其他线段，不再标注或使用其他字母，不必写出证明过程）
综合与应用
24、（本小题满分12分）
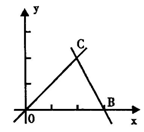
如图，直线OC、BC的函数关系式分别是y1=x和y2=-2x+6，动点P（x，0）在OB上运动（0<x<3），过点P作直线m与x轴垂直．
（1）求点C的坐标，并回答当x取何值时y1>y2？
（2）设△COB中位于直线m左侧部分的面积为s，求出s与x之间函数关系式．
（3）当x为何值时，直线m平分△COB的面积？
25、（本小题满分12分）
如图，A、B两点分别位于一个池塘的两侧，池塘西边有一座假山D，在DB的中点C处有一个雕塑，张倩从点A出发，沿直线AC一直向前经过点C走到点E，并使CE=CA，然后她测量点E到假山D的距离，则DE的长度就是A、B两点之间的距离．
（1）你能说明张倩这样做的根据吗？
（2）如果张倩恰好未带测量工具，但是知道A和假山、雕塑分别相距200米、120米，你能帮助她确定AB的长度范围吗？
（3）在第（2）问的启发下，你能“已知三角形的一边和另一边上的中线，求第三边的范围吗？”请你解决下列问题：在△ABC中，AD是BC边的中线，AD=3cm，AB=5cm，求AC的取值范围．
