八年级数学（上）寒假作业

八年级数学（上）寒假作业

今天是　　 年　月  日，星期　　，完成时间是　　 　　

　　　

基础练习

一、填空题

1、等腰三角形的______　　_、______　 __、　　　　_　　　　　　　 三线合一。

2、等腰三角形的一个角为50°,则顶角是　　　 度。

3、周长为13，边长为整数的等腰三角形有　　　个，

三边长分别　　　　　　　　　　　　　　　　 。

4、下列三角形不是直角三角形的是　 　　　　　 。

①　　  三角形三边长分别为5、12、13　 

②　　  三角形中有一边上的中线等于这边的一半

③　　  三角形的三个内角比为1：2：3　

④　　  三边之比为1，

⑤　　  三角形的三个内角比为1：1：2

⑥　　  三角形的三边之比为1：1：2

⑦　　  三角形的三边为3²，4²，5²

5、等腰三角形的底边长为10,则腰长m的取值

范围是____　　　　_____。

6、如图①所示，用一根长度足够的长方形纸带，先对折长方形得折痕l,再折纸使折线过点B，且使得A在折痕l 上，这时折线CB与DB所成的角为：　　　　  。

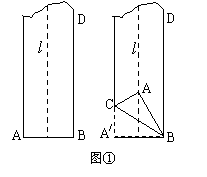
7、等边三角形按顺时针旋转最小角度是　　　 时，

图形与原图形重合。

二、选择题

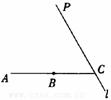
8、如图，B是线段AC的中点，过点C的直线l与AC成60⁰的角，在直线上取一点P，使∠APB＝30⁰，则满足条件的点P的个数是　　　　　　　　　　　  (　　　)

A. 3个　　　B. 2个　　C. l个　　D.不存在

9、下列说法错误的是　　　　　  　　　　 ( 　　 )

A.等腰三角形底边上的高所在直线是对称轴；

B.等腰三角形底边上的中线所在直线是对称轴；

C.等腰三角形顶角的平分线所在直线是对称轴；

D.等腰三角形一内角平分线所在直线是对称轴。

10、等腰三角形两边长为2和7,则周长是　 (　 　 )

A.9　　B.11　　C.16　　D.11或16

11、将直角三角形的三边长都扩大同样的倍数后，得到的三角形是　　　　　　　　　　　　　　　 （　　 ）

A.仍为直角三角形 　 B.可能是锐角三角形

C.可能是钝角三角形　D.不可能直角三角形

12、等腰三角形周长为12,腰长a的取值范围( 　　 )

  A.a>6　  B.a<3　  C.4<a<7　  D.3<a<6

　　  数学探究

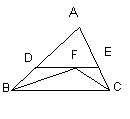
13、如图,在△ABC中,已知∠B和∠C的平分线相交于点F,过点F作DE∥BC交 AB于D,交AC于E,若BD+CE=9,求线段DE的长。

14、给出一组式子：3²+4²=5²　　8²+6²=10²　

15²+8²=17²　 24²+10²=26²　　35²+12²=37²

(1)　 请写出第六个式子:　　　　　　　　 。

(2)　 请用含有n的式子描述你发现的规律,

试说明你所发现规律的正确性。

15、△ABC的三边为a、b、c，且满足条件：

a²c²－b²c²=a⁴－b⁴，试判断三角形的形状。

解：∵a²c²－b²c²=a⁴－b⁴ ①

c²(a²－b²)=(a²+b²)(a²－b²)　　②

∴c²=a²+b² ③

∴△ABC为直角三角形 　　　　④

上述解答过程中代码_________出现错误；

正确答案应为△ABC是_________三角形。

拓展创新

16、如图（1），△ABC中，∠BAC=90°，AB=AC，过A点有一条直线l，且B、C在AE的同侧，作BD⊥AE于D、CE⊥AE于E。

 （1）请说明DE=BD+CE的理由；

 （2）若直线l绕A点旋转到图（2）的位置时（BD＞CE），其余条件不变，则DE、BD、CE之间有怎样的关系？（不需说明理由）

 （3）若直线l绕点A旋转到图（3）的位置，其余条件不变，问DE与BD、CE有怎样的关系？并说明理由。　　　　　　　　　　　　　　 　　　　　　　　　　　 

　　　 (1)　　　　　　　　　　　　　 (2)

(3)

数学乐园

总统巧证勾股定理

学过几何的人都知道勾股定理．它是几何中一个比较重要的定理，应用十分广泛．迄今为止，关于勾股定理的证明方法已有500余种．其中，美国第二十任总统伽菲尔德的证法在数学史上被传为佳话．总统为什么会想到去证明勾股定理呢？难道他是数学家或数学爱好者？答案是否定的．事情的经过是这样的；在1876年一个周末的傍晚，在美国首都华盛顿的郊外，有一位中年人正在散步，欣赏黄昏的美景，他就是当时美国俄亥俄州共和党议员伽菲尔德．他走着走着，突然发现附近的一个小石凳上，有两个小孩正在聚精会神地谈论着什么，时而大声争论，时而小声探讨．由于好奇心驱使伽菲尔德循声向两个小孩走去，想搞清楚两个小孩到底在干什么．只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形．于是伽菲尔德便问他们在干什么？只见那个小男孩头也不抬地说：“请问先生，如果直角三角形的两条直角边分别为3和4，那么斜边长为多少呢？”伽菲尔德答到：“是5呀．”小男孩又问道：“如果两条直角边分别为5和7，那么这个直角三角形的斜边长又是多少？”伽菲尔德不加思索地回答到：“那斜边的平方一定等于5的平方加上7的平方．”小男孩又说道：“先生，你能说出其中的道理吗？”伽菲尔德一时语塞，无法解释了，心理很不是滋味。

于是伽菲尔德不再散步，立即回家，潜心探讨小男孩给他留下的难题。他经过反复的思考与演算，终于弄清楚了其中的道理，并给出了简洁的证明方法。

他是这样分析的，如图所示：

　　　　　　　　　　　　　　　

　 　

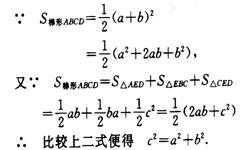
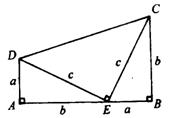
1876年4月1日，伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。

1881年，伽菲尔德就任美国第二十任总统后来，人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明，就把这一证法称为“总统。”证法。