八年级上期期中数学测试题
（时间120分钟 总分150分）
班级__________学号________姓名_______________总分_____________
一、选择题（每小题4分，共40分）毛
1．下列点一定在函数y=
的图象上的是（ ）
A．（-2，2） B．（1，-1） C．（-1，-1） D．（0，0）
2．已知点（-2，y1），（-1，y2），（1，y3）都在直线y=－
x+b上，则y1，y2，y3的值的大小关系是（ ）．
A．y1>y2>y3 B．y1<y2<y3 C．y3>y1>y2 D．y3>y1>y2
3. . 下列等式中正确的个数是 ( )
① m4＋m5＝m9 ② x2mxn＝x2mn ③ (m3)n(m2)n＝m5n ④ -a4(-a)2＝a6
A.1 B.2 C.3 D.4
4、若A ＝ a3－2a2＋a－7,B＝a3－3a2－5,C ＝ 5a2－7a＋8,则A＋B＋C的值为（ ）
A.2a3－10a2＋8a－20 B. 2a3－3a2－5
C. 2a3－10a2＋8a－4 D. 2a3＋8a＋4
5．下列因式分解错误的是 ( )
A．
B．
C．
D．
6. 下列多项式：①
②
③
④
，其中能用完全平方公式分解因式的有 ( )
A．1个
B．2个 C．3个 D．4个
7．一天，王老师从学校坐车去开会，由于途中塞车，他只好步行赶到会场，开完会后，他直接回到学校，下图中能体现他离学校的距离y（千米）与时间x（时）的关系的图象是（ ）
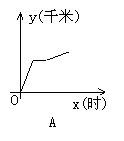
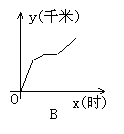
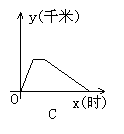
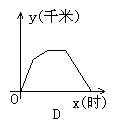
8. 当
时，函数y=ax+b与
在同一坐标系中的图象大致是（ ）.
 |
A. B. C. D
9. 已知a.b.c为三角形ABC的三边,且满足a2＋b2＋c2－ab－ac－bc＝0,则三角形的形状是( ) A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.等边三角形
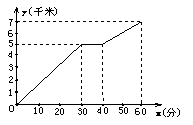
10．如图3是一名同学骑自行车出行的图象，从图象得知正确的信息是（ ）
A．整个行进过程中的平均速度是
千米/时; B．前20分钟的速度比后半小时速度慢
C．该同学在途中停下来休息了10分钟; D．从起点到终点该同学共用了50分钟
二、填空题（每小题3分，共39分）
11．函数
的自变量x的取值范围是
.
12.3xy－5x4＋6x－1是关于x 的 次 项式；按x降幂排列是 ；
13. 写出同时具备下列两个条件的一次函数表达式（写出一个即可）_________
（1）y随着x的增大而减小。（2）图象经过点（1，-3）
14. 函数y=kx+b（k≠0）的图像与函数y=－
x+3的图像平行，且与y轴的交点为M（0，2），则kx+b=0的解为____________
15. 已知一次函数y1=（m2-2）x+1-m与y2=（m2-4）x+2m+3的图像与y轴交点的纵坐标互为相反数，则m的值为___________
16. 已知一次函数y=kx+b,且当－1≤x≤2时, y的最大值为2,最小值为1,则这个一次函数的解析式为___________
17. －2x2y2 m+3 n与x3 m+2 ny3是同类项，则 m ＝ ，n＝ ；
18. 若2x+y=3，则4x·2y=________．若m2+m-1=0，则m3+2m2+2001=_______．
19. 若4x2+kx+121是一个完全平方式，则k=________．
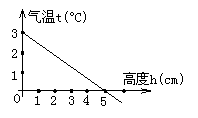
20．如图4是某地气温t（℃）随着高度h（千米）的增加而降低的关系图，观察图象可知该地地面气温是_______℃；当高度超过_______千米时，气温就会低于0℃．
21.计算(x2＋mx＋8)(x2－3x＋n)展开式中不含x2和x3的项，则m＝_________,n＝________
22. 已知－x3＋4x2＋2xy2－8xy＝0，则x ＝ ，y＝ ；
23．某商店出售货物时，要在进价的基础上增加一定的利润，下表体现了其数量x（个）与售价y（元）的对应关系，根据表中提供的信息可知y与x之间的关系式是_______________．
| 数量x（个） | 1 | 2 | 3 | 4 | 5 |
| 售价y（元） | 8.2 | 16.4 | 24.6 | 32.8 | 41.0 |
三、解答题（共81分，其中23、24题的1、2小题每小题4分，第3小题5分）
23.计算 (1) 
（2）（5x+3y）（3y-5x）-（4x-y）（4y+x）
（3）．解方程组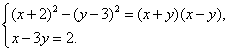
24．因式分解（1）
（2）（x2+4）2-16x2
25．（8分）已知y=y1+y2，y1与x成正比例，y2与x-1成正比例，且x=3时y=4；x=1时y=2，求y与x之间的函数关系式，并在直角坐标系中画出这个函数的图象．
26.（10分）先化简再求值：
，其中
，
．
27、（10分）已知：x2－3x＋1＝0，求：①x2 ＋ x-2 ② ( x － x-1 )2 ③ x4 ＋ x-4
28．(10分)已知直线y1= k1x +b1经过原点O和点（－2，－4），直线y2= k2 x+b2经过点（1，5）和（8，－2） ①求y1，y2的函数解析式，并画出函数图象 ②若两直线相交于点M，求点M的坐标 ③若直线y2与x轴交于点N，试求△MON的面积
29（8分）阅读材料，大数学家高斯在上学读书时曾经研究过这样一个问题：1+2+3+…+100＝？经过研究，这个问题的一般性结论是1+2+3+…+
其中ｎ是正整数。现在我们来研究一个类似的问题：1×2+2×3+…
＝？观察下面三个特殊的等式
、
、
将这三个等式的两边相加，可以得到1×2+2×3+3×4＝
读完这段材料，请你思考后回答：⑴
_______________
⑵
___________
(3)证明（2）的正确性
29．（14分）火车站有甲种货物1530t，乙种货物1150t，安排一列火车运往广州，这列火车可拉A，B两种规格不同的车厢50节，已知一节A型车厢的运费是0.5万元，一节B型车厢的运费是0.8万元。
①设这批货物的总运费是y（万元），用A型车厢x节，写出y与x之间的函数关系式
②已知35t甲种货物与15t乙种货物可装满一节A型车厢，2t甲种货物与35t乙种货物可装满一节B型车厢，按此要求安排A，B两种车厢的节数，有哪几种装运方案？
③利用一次函数的性质，研究在这些方案中，哪种方案运费最少？最少运费是多少？