八年级上学期期末数学模拟检测
姓名： 班级： 学号： 分数：
一．选择题（本题共13小题，每题3分，共39分）
1．下列运算中，错误的是（ ）
A．
B．
C．
D．
2．如下左图，所列图形是旋转对称图形的有( )个.
A．3个 B．4个 C．5个 D．6个
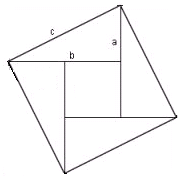
3、如上面右图是我国古代数学家赵爽所著的《勾股圆方图注》中所画的图形，它是由四个相同的直角三角形拼成的，下面关于此图形的说法正确的是（ ）
A．它是轴对称图形，但不是中心对称图形B．它是中心对称图形，但不是轴对称图形
C．它既是轴对称图形，又是中心对称图形D．它既不是轴对称图形，又不是中心对称图形
4、 有六个数:0.125125…, 0.,-
, 
, 
，
其中无理数有 ( )个
A 2 B
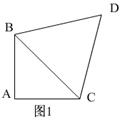5、已知，如图1，
中，
，若
为等边三角形，则四边形
的周长为（ ）
A、
； B、
； C、
； D、
；
6、下列说法中正确的是…………………………………………（ ）
A．矩形的对角线互相垂直 B．.菱形的对角线相等
C．正方形的对角线相等且互相平分 D．等腰梯形的对角线互相平分
7、如图，平行四边形ABCD中，CE垂直于AB，∠D＝
，
则∠BCE的大小是………………………………（ ）
A. B.
C.
D.
8、如图1，△DEF是由△ABC经过平移后得到的，
则平移的距离是（ ）
A、线段BE的长度 B、线段EC的长度
C、线段BC的长度 D、线段EF的长度
9、把多项式
分解因式等于（ ）
A、
B、
C、m(a-2)(m-1) D、m(a-2)(m+1)
10、□ABCD的周长是18，△ABC的周长是14，则对角线AC的长是（ ）
A 5 B
11、若正方形的一条对角线为10，则这个正方形的面积为（ ）
A 100 B
12如(x+m)与(x+3)的乘积中不含x的一次项，则m的值为（ ）
A.
–3 B.
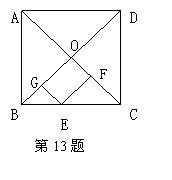
13、如图,正方形ABCD的边长为1,E为BC上任意一点,EF⊥AC于F,
EG⊥BC于G,则EF+EG的值为……………………( )
A.2
B. 
C.3
D.
二．填空题（本题共7小题，每题3分，共21分
1、81的平方根是 ，立方根是 ；
2、计算：
；
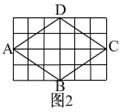
3、已知，如图2，网格中每个小正方形的边长为1，则四边形
的面积为
；
4、若
x+y=6，则3x-3y=__________.
5、已知菱形一对角线长是12cm，它与一边的夹角为60°，则菱形的边长为 .
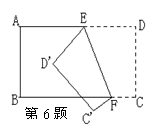6、如图，把一个长方形纸片沿EF折叠后，点D、C分别在D′、C′位置，若∠EFB=65°，则∠AED′=_________.
7、计算：
；
；分解因式：
=
。
三、解答题：
1、（本题6分）对下列代数式分解因式：
（1）4x
－4x
＋x
（2） 
2、（本题4分）已知
，
求：（1）
；（2）
的值。
3、（本题4分）化简后求值：
其中：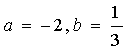
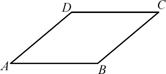4、（本题5分）
如图，在□ABCD中，已知∠A＝40°，求其他各个内角的度数．
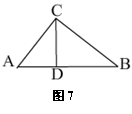5、（本题5分）已知，如图7，在
中， 
，
，
，求斜边
上的高
；
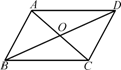
6、 （本题5分）如图，在平行四边形ABCD中，已知AC、BD相交于点O，两条对角线的和为26厘米，CD的长为8厘米，求△ABO的周长．
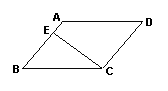
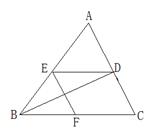7、（本题5分）如图，ΔABC中，BD平分∠ABC，DE∥BC，EF∥AC，试确定CF与BE的大小关系，并说明理由.
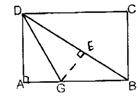
8、（本题6分）如图，折叠长方形纸片ABCD，先折出折痕（对角线）BD，在折叠，使AD落在对角线BD上，得折痕DG，若AB=4，BC=3，求AG。
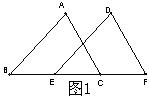
附加题：（本题10分）在图1至图3中，已知△ABC的面积为a．
（1）如图1，延长△ABC的边BC到点D，使CD=BC，连结DA．若△ACD的面积为S1，则S1=______（用含a的代数式表示）；
（2）如图2，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连结DE．若△DEC的面积为S2，则S2=__________（用含a的代数式表示）；
（3）在图1—2的基础上延长AB到点F，使BF=AB，连结FD，FE，得到△DEF（如图3）．若阴影部分的面积为S3，则S3=__________（用含a的代数式表示），并运用上述（2）的结论写出理由．
理由: