八年级上学期数学期中考试
班级 学号 姓名 得分
一、选择题（每小题3分，共30分）
1、在下列实数中： 
，
，－3，
，0.8…，
无理数的个数有（ ）个
A、1 B、2 C、3 D、4
2、与数轴上的点一一对应的数是（ ）
A、实数 B、有理数 C、无理数 D、整数
3、下列命题正确的是（ ）
A、两组对边分别平行的四边形是矩形 B、有一个角是直角的平行四边形是矩形
C、有两个角是直角的四边形是矩形D、有一个角是直角，一组对边平行的四边形是矩形
4、正方形的对角线具有（ ）
A、平分 B、垂直 C、相等 D、垂直、平分且相等
5、下列图案既是中心对称图形，又是轴对称图形的是 （ ）
 |
A. B. C. D.
6、下列说法错误的是（ ）
A、1是(－1)2的算术平方根 B、
C、－27的立方根是－3 D、
7. 下列说法：
①有理数与数轴上的点一一对应；
②有一条对角线平分一组对角的平行四边形是菱形；
③直角三形的两边长是5和12，则第三边长是13；
④近似数1.5万精确到十分位；
⑤平行四边形既是轴对称图形，也是中心对称图形.
其中错误说法的个数是………………………………………………………………( )
A、5个 B、4个 C、3个 D、2个
8. 如图，正方形网格中的△ABC，若小方格边长为1，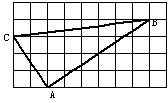
则△ABC是 （ ）
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 以上答案都不对
9、将直角三角形三边扩大相同的倍数，得到的三角形是（ ）
（A）锐角三角形 （B）钝角三角形 （C）直角三角形 （D）任意三角形
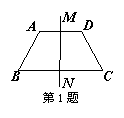
10. 如图，梯形ABCD中，AD∥BC，AB＝CD＝AD＝1，∠B＝60°，直
线MN是梯形的对称轴，P为直线MN上的一动点，则PC＋PD的最小值
为_______.
A、1
B、 
C、
D、2
二、填空题：（每空2分，共22分）
1、
的平方根是
2、一条线段AB的长是3cm，将它沿水平方向平移4cm后，得到线段CD，
CD的长是
3、若一个多边形的内角和等于它的外角和的3倍，则它是 边形
4、Rt△ABC 中，∠C=90 并且AC=5cm，AB=13cm，则BC= cm
5、平行四边形两邻角的比是3∶2，则这两个角的度数分别是
6、AC、BD是菱形的对角线，且AC=6cm，BD=8cm，则此菱形的面积是 cm2
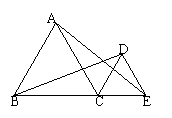7、△ABC和△DCE是等边三角形，则在右图中，△ACE
绕着 __ 点 __ 旋转 __ 度可得到△BCD。
8、矩形ABCD的周长是56cm，对角线AC、BD相交于点O，
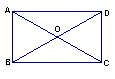△OAB与△OBC的周长差是4cm，则矩形ABCD
中较短的边长是 。
9、若ABC的三边分别是a、b、c，且a、b、c
满足(a+b)2－2ab=c2，则△ABC为 三角形
10、如图（1），以左边图案的中心为旋转中心，将
图案按 方向旋转 即可得到右边图案。
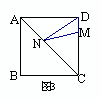
11、已知：如图3,正方形ABCD的边长为８,Ｍ在DC上，且DM＝２,N是对角线上的一动点，则DN+MN的最小值为___________
三、作图题（共6分）
将左图绕O点逆时针旋转
，将右图向右平移5格。
 |
四、解答题（共42分）
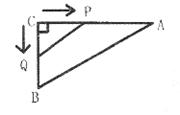
1、 (5分)某人欲从A点横渡一条河，由于水流的影响，实际上岸地点
 |
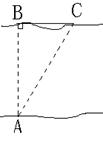C偏离欲到达点B 240米，结果他在水中实际游了510米，求该河的宽度。
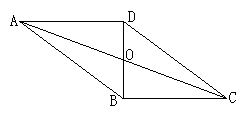
2、（6分）如图，□ABCD的周长是36，且AB∶BC＝5∶4，对角线AC、BD相交于点O，且BD⊥AD，求OB的长。
3、如图，在平行四边形ABCD中，点E、F在对角线AC上，且AE=CF
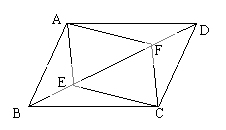求证：四边形BEDF是平行四边形（6分）
4、如图，E是正方形ABCD边AB的中点，DF⊥CE于点M.说明：AM＝AD（7分）
 | |||
| | |||
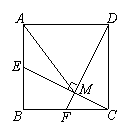5．(8分)如图，在△ABC中，AB=100cm，BC=60cm，∠C=90°，点P、Q同时从点C出发，分别沿CA、CB向点A、B运动。点P的速度为5cm／s，点Q的速度为4cm／s，
(1)当运动时间为4秒时，求四边形PABQ的面积；
(2)试问运动时间为几秒时，四边形PABQ的面积是△ABC面积的
?
6.(10分)如图，等腰梯形ABCD中，AD∥BC，AB=DC，对角线AC和BD交于点O，BC=8cm，BD=6cm，梯形的高为3cm．E是BC边上的一个动点（点E不与B、C两点重合），EF∥BD交AC于点F，EG∥AC交BD于点G．
⑴如图①，在点E运动过程中，试猜测GE、EF的长度和有什么特点?说明你的理由.
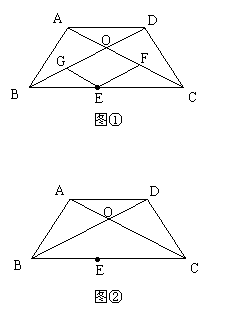⑵如图②，在点E运动过程中，若点E到BD、AC的垂线段分别为EP、EQ，你能确定EP+EQ的值吗？