八年级第一学期期中考试数学试题
（考试时间：120分钟 满分：100分）
| 题号 | 一 | 二 | 三 | 总分 | |||||||
| 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||||
| 得分 | |||||||||||
一、 填空题(每题2分,共24分)
1.已知函数y=3x－6，当x=0时，y=______;当y=0时，x=______.
2、已知一次函数y=kx+2过点（5，4）则k= ，
3、每盒铅笔有12枝，共售1.8元，铅笔售价y（元）与铅笔枝数x之间的关系式是
4.已知一次函数y=(k－1)x+5随着x的增大，y的值也随着增大，那么k的取值范围是______.
5．某中学举行一次演讲比赛，分段统计参赛同学的成绩，结果如下表：
| 分数段/分 | 60~69 | 70~79 | 80~89 | 90~100 |
| 人数/名 | 2 | 8 | 6 | 4 |
已知成绩在90分~100分的同学为优胜者，那么优胜率为
6.如果函数 
是正比例函数，则m＝
7．七（1）班一次数学测试成绩优秀的有20人，良好的有15人，及格的有5人，没有不及格的同学，制成扇形统计图时，成绩优秀的所占圆心角的度数是______，良好的所占圆心角的度数是_____ _．
8．把一组64个数据的样本分成8组，从第一组到第四组的频数分别为4、5、10、12，第五组到第七组的频率都是0.125，则第八组的频率为 ．（精确到0．01）
9．已知A（2，a）是函数y=2x+m与y=mx-2的图象的公共点，则m=_______，a=_______．
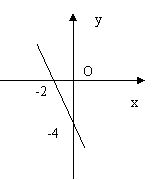
10．一次函数y=-2x-4的图像如图所示，
不等式-2x-4＜0的解集是 。
11、已知一次函数y=kx+b的图象经过（3，-3），且与直线y=－5x－3平行，则此一次函数的解析式是
12、在△ABC中，AB＝AC，其周长为15cm，则底边长y与腰长x之间的函数关系式为________，自变量x的取值范围是________．
二、选择题:(每题3分,共15分)
13．函数 
中，自变量x的取值范围是（ ）
A．x＞3． B．x＜3． C．x≥3． D．x≤3．
14.函数y=3x+1的图象通过（ ）
A.（3，5） B.（－2，3） C.（2，7） D.（4，10）
15．如图所示的图象分别给出了x与y的对应关系，其中y是x的函数的是（ ）
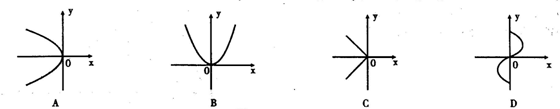
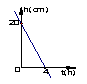
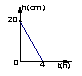
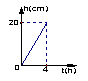
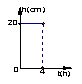16、一支蜡烛长20cm,点燃后每小时燃烧5cm,燃烧时剩下的高度h(cm)与燃烧时间t(h)的函数关系用图象表示为( )
 | |||
 | |||
(A) (B) (C) (D)
17.能清楚地看出各部分与总数之间的百分比关系的是( )
A．条形统计图．B．扇形统计图． C．折线统计图. D．以上都可以．
三、解答题：（61分）
18．下面是两个班的成绩统计图：(7分)
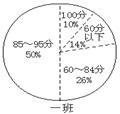
（1）如果85分以上为优秀，分别计算两班的优秀率：
一班优秀率：______________二班优秀率：______________
哪班的优秀率高？
（2）指出一班人数最多的扇形的圆心角的度数．
（3）这两个班的及格率分别是多少？
19.如图一次函数y =kx+b的图象经过点A和点B.(共6分)
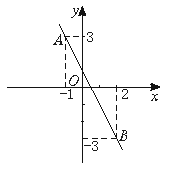
(1)写出点A和点B的坐标并求出k、b的值; (4分)
(2)求出当x=
时的函数值. (2分)
20．如图，用长为40m的竹篱笆围成一个长方形的鸡场，鸡场的一边靠墙（墙长18m），另三边用竹篱笆围成．设养殖场宽AB为x（m），面积为 y（ 
），求：(7分)
（1）y与x的函数关系式．(5分)
（2）x的取值范围．(2分)
21．为加强公民节约用水，减少污水排放的环保意识，某城市制定了以下用水收费标准（含城市污水处理费）：每户每月用水未超过8
时，按1.2元/收费；每户每月用水超过8时，其中的8仍按原标准收费，超过部分按1.9元/收费．设某户每月用水量为x()，应交水费为y(元)．（7分）
（1）分别写出用水未超过8和超过8时，y与x之间的函数关系式；（4分）
（2）某用户五月份共交水费13.4元，问该用户五月份用水多少立方米．（3分）
22、已知直线y=-3x与y=2x+5：（8分）
（1）求直线y=2x+5与y轴的交点坐标；（2分）
（2）求两条直线y=-3x、y=2x+5的交点坐标；（3分）
（3）求直线y=-3x与y=2x+5及y轴围成的三角形的面积。（3分）
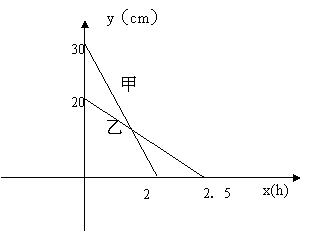
23、在一次蜡烛燃烧实验中，甲、乙两根蜡烛燃烧时剩余部分的高度y（cm）与燃烧的时间x(h)的关糸如图，请根据图象所提供的信息解答下列问题：（8分）
（1）甲、乙两根蜡烛燃烧前的高度分别是 ，从点燃到燃尽所用的时间分别是 （2分）
（2）分别求出甲、乙两根蜡烛燃烧时，y（cm）与x(h)之间的函数关系式（4分）
（3） x为何值时，甲、乙两根蜡烛燃烧过程中的高度相等？（2分）
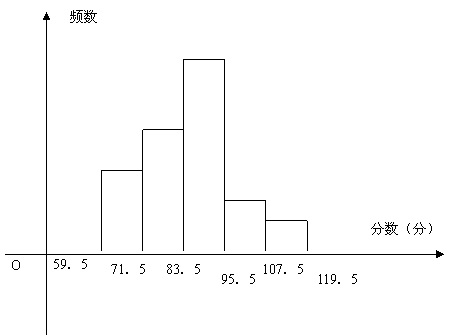
24我市某区对参加市模拟考试的8000名学生的数学成绩进行抽样调查，抽取了部分学生的数学成绩（分数为整数）进行统计，绘制成频率分布直方图，如图已知从左到右五个小组的频数之比依次是6：7：11：4：2第5小组的频数是40。（8分）
（1） 本次调查共抽取了多少名学生？（2分）
（2） 若72分以上（含72分）为及格，96分以上（含96分）为优秀，那么抽取的学生中及格人数，优秀人数各占所抽取的学生数的百分之几？（3分）
（3） 根据（2）中的结论，该区所有参加模拟考试的学生的及格人数，优秀人数各约多少人？（3分）
25（10分）A市和B市分别有某种库存机器12台和6台，现决定支援C村10台和D村8台，，已知从A市调运一台机器到C村和D村的运费分别是400元和800元，从B市调运一台机器到C村和D村的运费分别是300元和500元
（1） 设从B市运往C村机器x台，求总运费W（元）关于x的函数关系式（5分）。
（2） 若要求总运费不超过9000元，共有几种方案？（3分）
（3） 求出总运费最低的调运方案，最低运费是多少元？（2分）