八年级（上）数学阶段性测试试卷（12月份）
班级 学号 姓名
一、基本知识与基本技能（本题有10小题，每小题3分，共30分）。
1．在函数y= 中,自变量的取值范围是___ _____。
2. 点P(-5,1)沿x轴正方向平移2个单位,再沿y轴负方向平移4个单位,所得到的点的坐标为 。
3．三角形三边长分别为4，1-2a，7，则a的取值范围是 。
4．请你写出一个图象经过点（－1，2），并且y随x的增大而增大的一次函数的解析式：_______________。
5．有10个数据的平均数为6，另有20个数据的平均数为3，那么所有这30个数据的平均数是________。
6．若直线y=kx+b经过第一、二、四象限，则k,b的取值范围是k____0,b____0 。
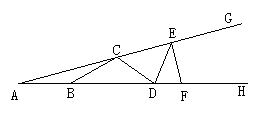7．如图所示，C、E和B、D、F分别在∠GAH的两边上，且AB=BC=CD=DE=EF，若∠A=18°，则∠GEF的度数是________。
 |
|
8.已知关于
的不等式组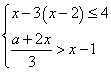
的解是
，则
=_________。
9．如上图，已知CA=CB，说出数轴上点A所表示的数是
。
10．如右图所示，用一根长度足够的长方形纸带，先对折长方形
得折痕l，再折纸使折线过点B，且使得A在折痕l 上，这时
折线CB与DB所成的∠DBC= 度。
二、选择题（本题有10小题，每小题3分，共30分）．
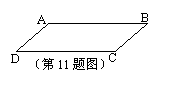11．如图，若AB∥CD,则有①∠A＋∠B＝180O②∠B＋∠C＝180O③∠C＋∠D＝180O；上述结论正确的是（ ）
A．只有① B．只有② C．只有③ D．只有①和③
12．分析下列说法：
①长方体、正方体都是棱柱；
②三棱柱的侧面是三角形；
③圆锥的三视图中:主视图、左视图是三角形，俯视图是圆；
④球体的三种视图均为同样大小的图形；
⑤直六棱柱有六个侧面、侧面为长方形。
其中正确的说法有（ ）种。
A.2 B.3 C.4 D.5
13．下列命题错误的是（ ）
A．等腰三角形两腰上的中线相等；
B．等腰三角形两腰上的高相等；
C．等腰三角形的中线与高重合；
D．等腰三角形顶角平分线上任一点到底边两端点的距离相等。
14．下列各点中，不在函数y=2x+1的图象上的是( )
A．(0,1) B．(1,3)
C．(-
,0 )
D．(-1,3)
|
A．14，14 B．15，14 C．14，15 D．15，16
16.已知x轴上的点P到y轴的距离为3,则点P的坐标为( )
A.(3,0) B.(0,3) C.(0,3)或(0,-3) D.(3,0)或(-3,0)
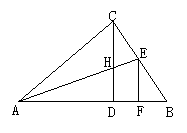
17．如图，Rt△ABC中，CD是斜边AB上的高，
角平分线AE交CD于H，EF⊥AB于F，则下列
结论中不正确的是（ ）
A．∠ACD=∠B B．CH=CE=EF C．CH=HD D．AC=AF
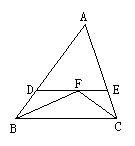18．如图，△ABC中，∠ABC与∠ACB的平分线交于点F，过点F作DE∥BC交AB于点D，交AC于点E，那么下列结论：
①△BDF和△CEF都是等腰三角形； ②DE=BD+CE；
③△ADE的周长等于AB与AC的和； ④BF=CF．
其中正确的有（ ）
A．①②③ B．①②③④ C．①② D．①
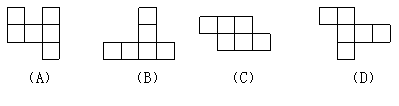19．下列各图中能折成正方体的是 ( )
20．已知点A(a+2,5)、B(-4,1-2a),若AB平行于x轴,则a的值为( )
A.-6 B.2 C.3 D.-2
三．解答题（本题有5小题，共40分）
21．（10分）已知一次函数的图象经过点A(-3,4),B(-1,-2)。
（1）求出这个一次函数的解析式，并作出它的图象；（2）求△AOB的面积；
（3）由图象观察，当-4≤x≤1时，函数y的变化范围.
22．（10分）解下列不等式(组).
(1) 
≤2
(2)
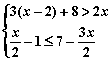
23．（6分）画出下图几何体的三视图。
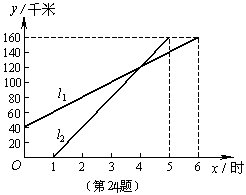24．（8分）一艘轮船从甲港出发到丙港，一艘快艇从乙港出发经甲港再沿着轮船的航线到丙港，图中l1，l2分别表示两船行驶的路程和时间的关系(其中快艇的速度大于轮船的速度)．根据图象回答下列问题：
(1) 轮船和快艇的速度分别是多少？
(2) 甲港、乙港到丙港的路程分别有多少千米？
(3) 求l1和l2所在直线的一次函数表达式；
(4) 快艇出发多少时间赶上轮船？
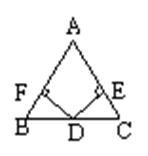25．（6分）如图，已知D是△ABC的BC边的中点，DE⊥AC，DF⊥AB，垂足分别为E，F，且DF=DE，则△ABC是等腰三角形吗？请说明理由．