八年级（上）数学期末试卷
一、填空题（每题3分，共30分）
1、36的平方根是 ，
的立方根是 ，
的绝对值是 。
2、已知三角形三边长分别是6，8，10，则此三角形的面积为 。
3、菱形有一个内角是60°，边长为5cm，则它的面积是 。
4、一个多边形的内角和等于1080°，那么这个多边形为 边形。
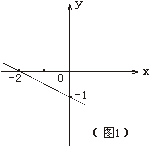
5、一次函数图象如图1所示，则函数关系式是 。
 |  |
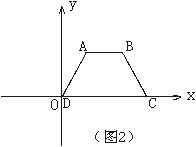6、如图2，等腰梯形ABCD中，∠ADC=60°，AB=2，CD=6，则各顶点的坐标是A（2，
），B ，C ，D（0，0）。
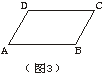7、如图3，已知，AD//BC，要使四边形ABCD是平行四边形，还需添
加条件 （只填写一个条件即可，不在图形中添加其他线段）
8、已知 是方程2x－ay=5的一个解，则a= 。
9、某班10位同学将平时积攒的零花钱捐献给贫困地区
的失学儿童，每人捐款金额（单位：元）依次为5，6，
10，8，12，6，9，7，6，8。这10名同学平均捐款
元，捐款金额的中位数是 元，众数是 元。
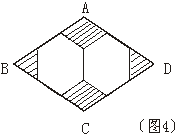
10、如图4，菱形花坛ABCD的周长为36cm，∠B=60°，其中由两个正六边形拼接而成的图形部分种花，其余“四个角”是绿草地，则种花部分的图形的周长（不计拼接重合的边）为 cm。
二、选择题（每题2分，共20分）
11、下列说法：（1）无尽小数都是无理数；（2）实数与数轴上的点一一对应；（3）任何实数都有平方根。（4）无理数就是带根号的数。其中说法错误的是（ ）
A、1 B、2 C、3 D、4
12、估算
（误差小于0.1）的大小是（
）
A、8 B、8.3 C、8.8 D、8.0～8.1
13、下列多边形能进行密铺的是（ ）
A、棱形 B、八边形 C、正五边形 D、十边形
14、直角坐标系中，点（－2，3）与（2，－3）关于（ ）
A、原点中心对称 B、Y轴轴对称 C、X轴轴对称 D、以上都不对
15、以下五个大写正体字母中，是中心对称图形的共有（ ）
G M S X Z
A、5 B、4 C、2 D、3
16、若方程x＋y=3，x－y=5和x＋ky=2有公共解，则k的值是（ ）
A、2 B、－2 C、1 D、3
17、将△ABC的三个顶点的横坐标乘以－1，纵坐标不变，则所得图形（ ）
A、与原图形关于Y轴对称 B、与原图形关于X轴对称
C、与原图形关于原点对称 D、向X轴的负方向平移了一个单位
18、已知正比例函数y=kx（k≠0）的函数值y随x的增大而增大，则一次函数y=x+k的图象大致是（ ）
 |
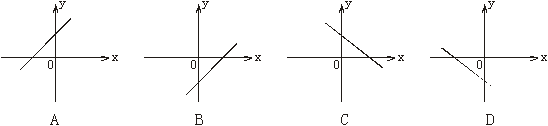19、下列命题正确的是（ ）
①对角线互相垂直且相等的平行四边形是正方形.
②平行四边形、矩形、等边三角形既是中心对称图形，也是轴对称图形。
③旋转和平移都不改变图形的形状和大小。
④底角是45°的等腰梯形，高是h，则腰长是 
h。
A、①②④ B、①③④ C、全对 D、①②③
20、某校八年级（2）班50名学生参加体育考试，平均分为60分，60分以上（含60分）为及格，及格人数人均70分，不及格人数人均45分，则及格人数为（ ）
A、10 B、20 C、30 D、35
三、解答题（50分）
21、化简（每题4分，共8分）
（1）
（2）
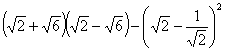
22、解方程组（每题6分，共12分）
（1）
（2）用图象法解方程组：
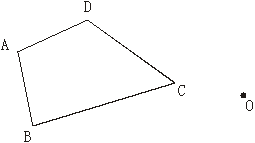
23、（6分）如图，四边形ABCD绕点O顺时针方向旋转90°，作出旋转90°后的图形（不写作图步骤，要求线条清晰，表示清楚）。
| 月份 | 用水量（吨） | 水费 （元） |
| 9 | 5 | 10 |
| 10 | 7 | 16 |
 |
24、（8分）某商场购进物品后，加价50%作为销售价。商场搞优惠促销，决定由顾客抽奖确定折扣，某顾客购买甲、乙两种商品，分别抽到八折和九折，共付款450元，两种商品原销售价之和为525，两种商品的进价分别为多少元？
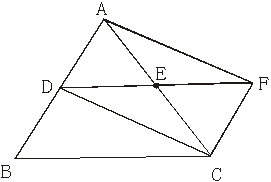
25、（8分）如图 ，在△ABC中，D、E分别是AB、AC边的中点，F是DE延长线上的点，且EF=DE，请找出图中的平行四边形，并说明理由。
26、（8分）为了增强公民的节水意识，合理利用水资源，某市规定用水收费标准：每户每月的用水量不超过6吨时，水费按每吨m元收费，超过6吨时，不超过部分仍按每吨m元收费，超出部分按每吨n元收费。该市某户今年9、10月份的用水量和所交水费如下表所示，设某户每月用水量x吨，应交水费y元。
（1）求m、n的值
（2）分别写出用水不超过6吨和超过6吨时，y关于x的函数关系式。
（3）若该户11月份用水10吨，求11月份应交水费。