八年级（上）数学期中考试试题
班级_____________ 学号_______ 姓名________ 成绩评定____________
一、看准了再选（每题3分共30分）
1．函数
的自变量
的取值范围是（ ）
Ａ．
Ｂ．
且
Ｃ． Ｄ．
且
2.直线y＝ax＋b（a＜0，b＞0）不经过（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
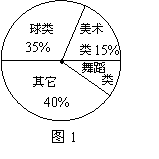
3．图1是某中学七年级学生参加课外活动人数的扇形统计图，若参加舞蹈类的学生有42人，则参加球类活动的学生人数有（ ）
Ａ．145人 Ｂ．147人 Ｃ．149人 Ｄ．151人
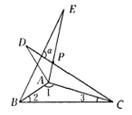
4．如图所示，△ABE和△ADC是△ABC分别沿着AB，AC边翻折180°形成的，若∠1∶∠2∶∠3=28∶5∶3，则∠α的度 数为（ ）
A．80° B．100° C．60° D．45°．
5．一辆汽车由
地匀速驶往相距300千米的
地，汽车的速度是100千米／小时，那么汽车距离B地的路程
（千米）与行驶时间
（小时）的函数关系用图象表示为（ ）
 |
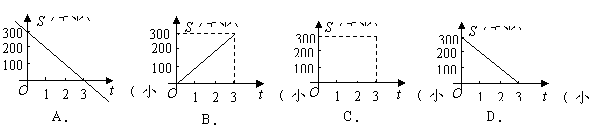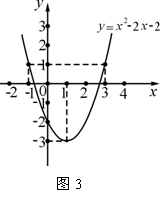
6．已知函数y=x2-2x-2的图象如图3所示， 根据其中提供的信息，可求得使y≥1成立的x的取值范围是（ ）
A．-1≤x≤3 B．-3≤x≤1 C．x≥-3 D．x≤-1或x≥3
7．学校把八年级900人的体重情况调查制成扇形统计图，发现体重在45～55千克对应的扇形圆心角的度数是126度，则体重在45～55千克范围内的学生有（ ）人．
A．315 B．310 C．280 D．270
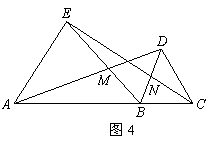
8．如图4，已知等边△AEB和等边△BDC在线段AC同侧，则下面错误的是（ ）．
A．△ABD≌△EBC B．△NBC≌△MBD C．DM=DC D．∠ABD=∠EBC
9．在平面直角坐标系内，直线y=
x+3与两坐标轴交于A、B两点，点O坐标原点，若在该坐标平面内有以点P（不与点A、B、O重合）为顶点的直角三角形与Rt△ABO全等，且这个以点P为顶点的直角三角形与Rt△ABO有一条公共边，则所有符合条件的P点个数为（
）．
（A）9个 （B）7个 （C）5个 （D）3个
10．如图5.2（
），在直角梯形
，
，
，动点
从
点出发，由
沿边运动，设点运动的路程为，
的面积为
，如果关于的函数的图象如图5.2（
），则
的面积为（ ）
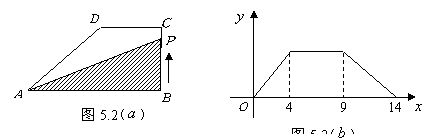Ａ．10 Ｂ．16 Ｃ．18 Ｄ．32
二、想好了再填（每题3分共30分）
1．一次函数的图象过点（-l , 0 ） ，且函数值随着自变量的增大而减小，写出一个符合这个条件的一次函数解析式: .
2．在△ABC中，∠C=900，AD平分∠CAB，BC=8cm，BD=5cm，那么D点到直线AB的距离是 cm。
3若直线y=kx＋b平行直线y=3x＋4，且过点（1，-2），则将y=kx＋b向下平移3个单位的直线是____________________
4．已知数据：25，22，21，25，19，26，22，28，24，27，25，26，26，27，29，28，36，24，25，30．在列频数分布表时，如果取组距为3，那么应分成________ 组，分别是__________．
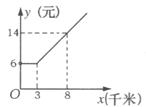
5. ．某市出租车公司规定：出租车收费与行驶路程关系如图所示．如果小明姥姥乘出租车去小明家花去了
元，那么小明姥姥乘车路程有__________千米．
6.如图，在和
中，
，若不添加任何字母与辅助线，要使
，则还需增加的一个条件是
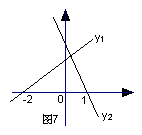
7.如图7是一次函数y1 = ax + b， y2 = kx + c的图象，观察图象，写出同时满足y1≥0，
y2≥0时x的取值范围____________________。
8.为了解教学情况，某校抽取了部分初三年级学生期末数学考试成绩，将所得分数整理后，画出频率分布直方图（分数取整数，满分120分），如图8所示，图中从左到右各小组的小长方形面积之比是5：16：13：9：7，第一小组的频数为10.
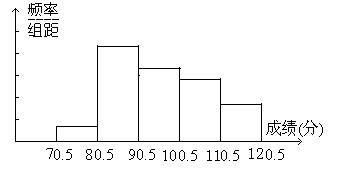
图8
请根据以上信息，回答下列问题：⑴第一小组的频率为_________；⑵在这个问题中，样本的容量是_____________；
⑶若分数在81分以上（含81分）为合格，试估计该校初三学生数学成绩的合格率是_____
三.理解了再写（共40分）
1．如图，在△ABC和△DEF中，B、E、C、F在同一直线上，下面有四个条件，请你从中选三个作为题设，余下的一个作为结论，写出一个正确的命题，并加以证明．
①
AB=DE，②AC
= DF，③∠ABC=∠DEF，④BE=CF．
已知：
求证：
证明：
2.请你根据图中图象所提供的信息解答下面问题：
(1)分别写出L1、L2中变量y随x变化而变化的情况：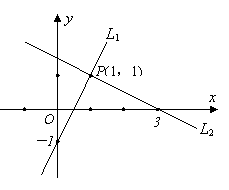
(2)求出一个二元一次方程组，使它满足图象中的条件。
3.地表以下岩层的温度t(0C)随着所处的深度h(千米)的变化而变化, t与h在一定范围内近似成一次函数关系
(1)根据下表,求t(0C)与 h(千米)之间的函数关系式;
(2)求当岩层温度达到7700C时,岩层所处的深度为多少千米?
| 温t(0C) | ··· | 90 | 110 | 300 | ··· |
| 深度h(千米) | ··· | 2 | 4 | 8 | ··· |
4. 如图，已知△ABC中，∠ACB=90°，AC=BC，AE是BC边上的中线，过C作CF⊥AE，垂足是F，过B作BD⊥BC交CF的延长线于D.
（1）求证：AE=CD；（2）若AC=12cm，求BD的长.
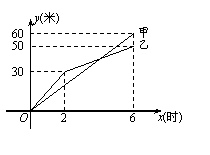5.有两段长度相等的河渠挖掘任务，分别交给甲、乙两个工程队同时进行挖掘．图中是反映所挖河渠长度y（米）与挖掘时间x（时）之间关系的部分图象．请解答下列问题：
（1）乙队开挖到30米时，用了_____小时．开挖6小时时，
甲队比乙队多挖了______米；
（2）请你求出：
①甲队在0≤x≤6的时段内，y与x之间的函数关系式；
②乙队在2≤x≤6的时段内，y与x之间的函数关系式；
③开挖几小时后，甲队所挖掘河渠的长度开始超过乙队？
（3）如果甲队施工速度不变，乙队在开挖6小时后，施工速度增加到12米/时，结果两队同时完成了任务．问甲队从开挖到完工所挖河渠的长度为多少米？
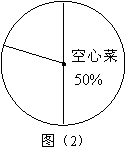6.图（1）是某中学九年级（一）班全体学生对三种蔬菜的喜欢人数的频数分布直方图．
解答下列问题：
（1）九年级（一）班总人数为 人；
（2）哪种蔬菜的喜欢人数频率最高？并求出该频率；
（3）请根据频数分布直方图中的数据，补全图（2）中的扇形统计图；
（4）根据上述统计的结果，请你为食堂的进货提出一条合理化的建议．
 |
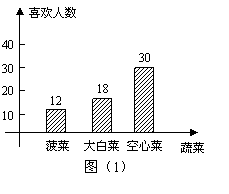7.商店出售茶壶和茶杯，茶壶每只定价20元，茶杯每只定价5元。该店制定了两种优惠办法：（1）买一只茶壶赠送一只茶杯；（2）按总价的92％付款。某顾客需购茶壶4只，茶杯若干只（不少于4只），若购买茶杯数为x（只）付款数为y（元），试分别建立两种优惠办法中y与x之间的函数关系式，并讨论该顾客买同样多的茶杯时，两种办法哪一种更省钱？