八年级（上）数学期中试卷
一、选择题（10×3分）
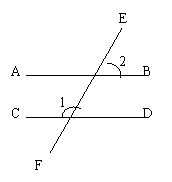
1.如右图，AB∥CD，如果∠1是∠2的2倍，那么∠1等于（ ）
(A)60° (B)90° (C)120° (D) 150°
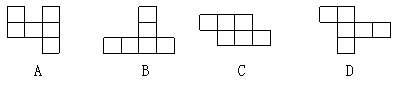2. 下列各图中能折成正方体的是( )
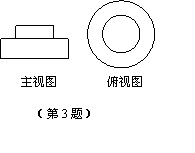3. 一天，小明的爸爸送给小明一个礼物，小明打开包装后画出它的主视图与
俯视图如图所示，根据小明画的视图，请你猜礼物是（ ）
A．钢笔 B．生日蛋糕 C．光盘 D．一套衣服
4.2、如图，边长为1的正方体中，一只蚂蚁从A顶点出发沿着
正方体的外表面爬到B顶点的最短路程是（ ）
(A)3 (B)
(C)2 (D)1
5. 等边三角形的对称轴有 （ ）
A、1条 B、2条 C、3条 D、4条
6.一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，那么两次拐弯的角度是（ ）
(A)第一次右拐50°，第二次左拐130°
(B)第一次左拐50°，第二次右拐50°
(C)第一次左拐130°，第二次左拐130°
(D)第一次右拐50°，第二次右拐50°
| 年龄 | 13 | 14 | 15 | 16 |
| 人数 | 4 | 22 | 23 | 1 |
7.八年级（1）班50名学生的年龄统计结果如表所示，则此班学生年龄的众数中位数分别为（ ）
(A)14，14 (B)15，14
(C)14，15 (D)15，16
8.分析下列说法中正确的有（ ）种
①长方体、正方体都是棱柱 ②球体的三种视图均为同样大小图形
③三棱柱的侧面是三角形 ④直六棱柱有六个侧面，侧面为长方形
⑤圆锥的三视图中，主视图、左视图是三角形，俯视图是圆
(A)2 (B)3 (C)4 (D)5
9.等边三角形按顺时针旋转最少角度是（ ）图形与厚图形重合。
(A)30° (B)90° (C)120° (D)60°
10. 以下列各数为边长，不能组成直角三角形的是（ ）
A、3，4，5 B、4，5，6 C、5，12，13 D、6，8，10
二、填空题（10×3分）
11．已知一个等腰三角形的两边长分别是2和5，那么这个等腰三角形的周长为 ；
12已知直角三角形的两直角边长为6cm和8cm，则斜边上的中线长是 cm
13．已知两条线段的长为5cm和12cm，当第三条线段的长为 cm，这三条线段能组成一个直角三角形。
14．等腰三角形一腰上的中线，将它的周长分成15cm和6cm两部分，则这个等腰三角形的底边上长是 cm。
15．小明帮助父母预算11月份电费情况，下表是11月初连续8天每天早上电表的显示读数：
| 日 期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 电表显示读数 | 21 | 24 | 28 | 33 | 39 | 42 | 46 | 49 |
如果每度电费用是0.53元，估计小明家11月（30天）的电费是 元。
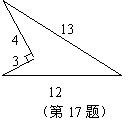16、如图，要为一段高为5米，长为13米的楼梯铺上红地毯，则红地毯至少要
|
米长；
17、有一块田地的形状和尺寸如图所示，则它的面积为 。
18．桌上摆着一个由若干个相同正方体组成的几何体，
其主视图和左视图如图所示，所以这个几何体最多
可以由___ _个这样的正方体组成。
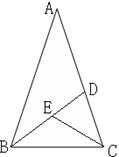
19.如图,AB=AC, ∠A=36°,BD、CE分别平分∠ABC、∠ACB,则图中等腰三角形个数是______
20、下面是五届奥运会中国获得金牌情况的一览表．
| 第23届 洛杉矶奥运会 | 第24届 汉城奥运会 | 第25届 巴塞罗那奥运会 | 第26届 亚特兰大奥运会 | 第27届 悉尼奥运会 |
| 15块 | 5块 | 16块 | 16块 | 28块 |
在15，5，16，16，28这组数据中，众数是__ ___，中位数是_ ____．
三、解答题（共40分）
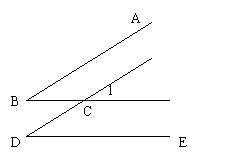21．如图，直线AB∥CD，DE∥BC，若∠B=（2x+15）°,∠D=(65－3x) °，求∠1的度数。（4分）
22．下表是两个商场1至6月份销售“椰树牌天然椰子汁”的情况(单位：箱)
| 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | |
| 甲商场 | 450 | 440 | 480 | 420 | 576 | 550 |
| 乙商场 | 480 | 440 | 470 | 490 | 520 | 516 |
根据以上提供的信息回答下列问题（6分）
（1）甲、乙两个商场月平均销售量哪个大？（2）甲、乙两个商场的销售哪个稳定？
23．如图，AD是等腰三角形ABC的底边BC上的高，DE∥AB，交AC于点E，判断△ADE是不是等腰三角形，并说明理由。（5分）
 |
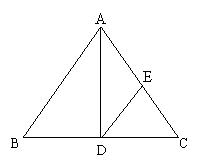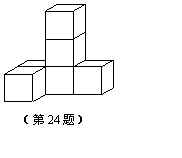
24．画出如图所示的几何体的三视图（6分）．
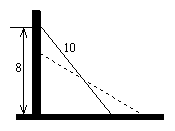
25. （8分）如果一个长为10m的梯子，斜靠在墙上，梯子的顶端距地面的垂直距离为8m．如果梯子的顶端下滑1m，请猜测梯子底端滑动的距离是否会超过1m，并加以说明．
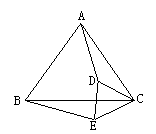
26、（8分）如图所示，已知 △ABC和△DEC是等边三角形．
（1） 请猜想线段AD和BE的大小关系；
（2） 证明你的猜想，并说明理由. 