八年级（上）数学期中试卷
班级 姓名 学号
一、选择题:(本题有10小题，每小题3分，共30分。)
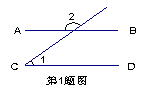
1. 如图，已知：AB∥CD，若∠1＝50°，则∠2的度数是（ ）
A、50° B、60° C、130° D、120°
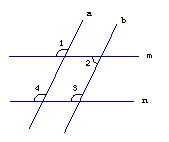
2. 如图，在下列条件中，能够直接判断
∥
的是（ ）
A．∠1=∠4 B．∠3＝∠4 C．∠2+∠3＝180° D．∠1＝∠2
3. 已知等腰三角形一边是3，一边是6，则它的周长等于（ ）
A．12 B．12 或15 C．15 D．18或15
4. 以下各组数据能作为直角三角形三边长的是 （ ）
A、6，11，12 B、5，11，12 C、6，12，13 D、5，13，12
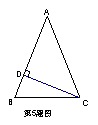
5. 如图，等腰三角形ABC中，AB=AC，∠A=44°，CD⊥AB于D，则∠DCB等于
A、44° B、68° C、46° D、22° ( )
6. 
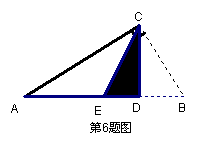
如图，CD是Rt△ABC斜边AB上的高，将△BCD沿CD折叠，B点恰好落在AB的中点E处，则∠A等于
（
） A．25° B．30° C．45° D．6°
第10题图
7. 
图1是小明用八块小正方体搭的积木，该几何体的俯视图是…………（
）
8.一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，那
么两次拐弯的角度是（ ）
A．第一次右拐50°，第二次左拐130°
B．第一次左拐50°，第二次右拐50°
C．第一次左拐50°，第二次左拐130°
D．第一次右拐50°，第二次右拐50°
9. 如果数据1、2、2、x的平均数与众数相同，那么x等于( )
（A）1 （B）2 （C）3 （D）4
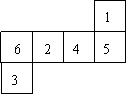
10. 下图可以沿线折叠成一个带数字的立方体，每三个带数字的面交于立方体的一个顶点，则相交于一个顶点的三个面上的数字之和最小是 ( )
（A） 7 （B） 8 （C） 9 （D） 10
二、填空题:(本题有8小题，每小题3分，共24分)
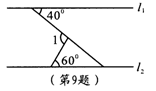
11. 如图所示，
，则
= 度。
12. 
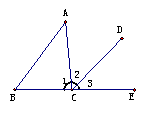如图，请填上你认为适合的一个条件：
，能使AB∥CD 。
（第12题图）
13. 某中学举行广播操比赛，六名评委对某班打分如下： 7.5分，8.2分，7.8分，9.0分，8.1分，7.9分．去掉一个最高分和一个最底分后的平均分是 分．
14. X1，X2，X3，X4，X5的方差为S2，则3X1+1，3X2+1，3X3+1，3X4+1，3X5+1的方差为 。
15. 等腰△ABC中，一腰AB的垂直平分线交另一腰AC于D，已知AB=12，△DBC的周长为20，则底边BC的长为 .
16. 一个正方体的每个面上都写有一个汉字，其平面展开图如图所示，那么在该正方体中，和“超”相对的字是 。
17．直角三角形的斜边长为10
，一直角边为8，则该三角形斜边上的高为___ __；
18．在直线l上依次摆放着三个正方形(如图所示)。已知斜放置的已一个正方形的面积分别是3，正放置的两个正方形的面积依次是S1、S2，则S1＋S2＝_______。
 |
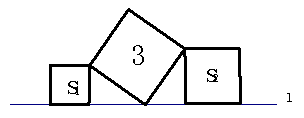（第18题图）
三、解答题:(本题有6小题，共46分)
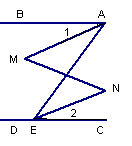
19． （本题6分）已知：如图，∠BAE+∠AED=180°，∠1=∠2，那么∠M=∠N.
下面是推理过程，请你填空：
解：∵∠BAE+∠AED=180°（已知），
∴ // （ ）
∴∠BAE=
（
）
又∵∠1=∠2（已知）
∴∠BAE-∠1= － ，
即∠MAE= ，
|
∴∠M=∠N（ ）
20．（每小题6分，共12分）
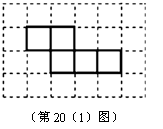⑴马小虎准备制作一个封闭的正方体盒子，他先用5个大小一样的正方形制成如下图所示的拼接图形(实线部分)，经折叠后发现还少一个面，请你在右图中的拼接图形上再接一个正方形，使新拼接成的图形
经过折叠后能成为一个封闭的正方体盒子.
(注：①只需添加一个符合要求的正方形；
②添加的正方形用阴影表示.)
⑵如图是一些小正方块所搭几何体的俯视图，小正方块中的数字表示该位置的小方块的个数，请画出这个几何体的主视图和左视图：
主视图
左视图
21．（本题6分）某运动鞋专柜在一天中销售的运动鞋尺码如下：
| 尺 码 | 17 | 21 | 22 | 23 | 24 |
| 数 量 | 1 | 1 | 5 | 2 | 1 |
（1）求销售的运动鞋尺码的平均数、众数和中位数；
（2）你认为该专柜应多进哪种尺码的运动鞋？
22．（本题6分）如图，小刚准备测量一条河的深度，他把一根竹
竿插到离岸边1.5米远的水底，竹竿高出水面
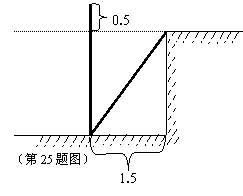0.5米，再把竹竿的顶端拉向岸边，竿顶和岸边
的水面刚好相齐；请计算并推断河水的深度为几米？
23.（本题8分）A B∥CD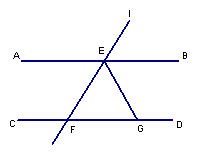
，直线
分别交AB、CD于点E、F，EG平分∠BEF，若∠EFG=40°，则∠EGF的度数是.
24.（本题8分）如图，已知在△ABC中，AB=AC，O是△ABC内一点，且OB=OC。求证：AO ⊥BC。
A
O
B C
| |
25．正三角形给人以“稳如泰山”的美感，它具有独特的对称性，请你用三种不同的分割方法，将下列三个正三角形分别分割成四个等腰三角形。（在图中画出分割线，并标出必要的角的度数）
 |  |  | |||