整式的加减

初二数学 § 15.1.2　整式的加减 　 编制日期 编者　　　　 　　　　　　　　　　 审核者　　　　　  班级______  学号______　 姓名___________　成绩评定______

一、基础练习：

1．下列代数式中：（1）3x²y和3a²b；（2）2a³b和-a³b；（3）4xyz和21yz；

（4）2.5x²y和0.5xy²；（5）6x²y和-yx²；（6）-1和3．其中是同类项的有（　）

　 A．（1）（2）（3）　　 B．（2）（4）（5）（6）

C．（2）（5）（6）　　 D．（4）（5）（6）

2．如果2x³ⁿy^m+4与-3x⁹y²ⁿ是同类项，那么m、n的值分别为（　）

　　A．m=-2，n=3　　B．m=2，n=3　　C．m=-3，n=2　　D．m=3，n=2

3．下列计算正确的是（　 ）

　 A、3a²+2a=5a²　 B、a²b+ab²=2a³b³ 　C、－6x²+x²+5x²=0　 D、5m－2m=3

4．下列去括号，正确的是（　）

A、-(a+b)=-a-b　　　　 B、－(3x-2)=－3x-2　

C、a²-(2a-1)=a²-2a-1　 D、x－2(y－z)=x－2y+z

5．化简a－(5a－3b)+(2b－a)的结果是（　 ）

 A、7a－b　　B、－5a+5b　　C、 7a+5b　　D、－5a－b

6．把一个两位数交换十位数字和个位数字后得到一个新的两位数，若将这个两位数与原两位数相加，则所得的和一定是（　 ）

 A、偶数　　B、奇数　　C、11的倍数　　D、9的倍数

7．一根铁丝正好可以围成一个长是2a+3b,宽是a+b的长方形框,把它剪去可围成一个长是a,宽是b的长方形(均不计接缝)的一段铁丝,剩下部分铁丝的长是(　　)

　A.a+2b;　　 B.b+2a;　　 C.4a+6b;　　 D.6a+4b

8．多项式2(x²-3xy-y²)-(x²+2mxy+2y²)中不含xy项,则m=(　 )

A、3　　B、－3　　C、 4　　D、-2

9．若－3x²y+ax²y=－6x²y,则a=　　　　　 .

10．化简代数式4x²-[7x²-5x-3（1-2x+x²）]的结果是__________．

11. 多项式3x³-x²y+xy²-y³与5x³-2x²y+3xy²的差是　　　　　　　　　 ．

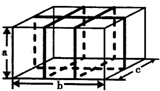
12．火车站和飞机场经常为旅客的行李提供“打包”服务，如果长、宽、高分别为a、b、c 的箱子按如图所示的方式“打包”至少需　　　　　　　　　   长的“打包”带。（图中粗线为“打包”带）

13．化简：

①（x²-2y²-z²）-（-y²+3x²-z²）+（5x²-y²+2z²）；　 ②- {2a²b-[3abc-（4ab²-a²b）]}

③ 5(x-y)⁵-(x-y)³-8(x-y)⁵-3(x-y)³ (整体思想)

14．先化简，再求值：

① 2x²-{-3x+5+[4x²-（3x²-x-1）]}，其中x=3．

② (5a²b+4b³-2ab²+3a³)-2(2a³-5ab²+3b³+2ab²),其中a=-2,b=3.

二．综合运用

1．若M,N都是4次多项式, 则多项式M+N的次数为(　　)

　A.一定是4　　  B.不超过4.　　C.不低于4.　 D.一定是8.

2．当x分别为2和－2时，3x²+4x⁴－x⁶+2的值（　 ）

 A、互为相反数　 B、互为倒数　 C、相等　 D、异号

3．已知x＜－2,则x+2－1－x=(　 )

 A、1　　B、－3　　C、2x+1　　D、－2x－1

4．设x表示两位数,y表示四位数,如把x放在y的左边组成一个六位数,用代数式表示为(　　)　　A. xy;　　B. 10000x+y;　　 C. x+y;　　D. 1000x+y

5. 对于有理数a,b,定义a⊙b=3a+2b,则[(x+y) ⊙(x-y)]⊙3x化简后得(　　)

　 A.0;　　B.5x;　　C.21x+3y;　　D.9x+6y

6. 多项式 与 的

差是　　　　　　　　　　　  .

7．当2y-x=5时，5（x-2y）²-3（-x+2y）-100的值是_________．

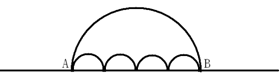
8. 图中有五个半圆，四个小圆的直径刚好在大圆的直径上，且直径之和等于大圆直径，两只小虫同时从点A出发，以相同的速度爬向点B，甲虫沿大圆圆周运动，乙虫沿其余四个小圆的圆弧的路线爬行，则下列结论正确的是（　 ）

A、甲先到点B　 B、乙先到点B　　　 C、甲、乙同时到达点B　 D、无法确定

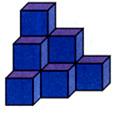
9.　10个棱长为a的正方体摆放成如上图所示的形状,这个图形的表面积是多少?

10.已知A=2a³-2a²+2a-1,B=3a³-3a²—4a-5,求当a=时,A-4(B-的值.