初二数学第三次月考试卷
出卷人：孔新国 审核：吴相生
一、 选择题：（2＇×10＝20＇）
1、
平方根是
（ ）
A、3 B、±3 C、
D、±
2、已知点P在第四象限,且到x轴的距离为3,到y轴的距离为2,则点P的坐标一定是 ( )
A、(－2 ,3 ) B、( 2 ,－3 ) C、(－3 ,2) D、(3 , －2)
3、已知点P(6 , －6),Q(－6 , －6),则直线PQ ( )
A、平行于x轴 B、平行于y轴 C、不平行于任何坐标轴 D、不能确定
4、若点M(a,b)在第四象限,则点N(－a ,－b+2)在 ( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
5、下列哪一个点在直线y=2x－3上 （ ）
A、（－2，3） B、（3， 2） C、（2，1） D、（－3，2）
6、直线y=x+3不经过哪个象限 （ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
7、拖拉机开始行驶时,油箱中有油4升,如果每小时耗油0.5升,那么油箱中余油y（升）与它工作的时间t（时）之间的函数关系的图象是 （ ）
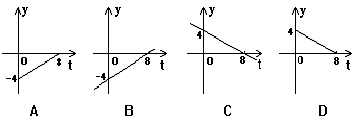
8、黄刚同学将一张正方形纸片撕成四张后，取其中一张再撕成四张，又取其中一张再撕成四张，如此继续下去，在下面给出的四个数据中，哪一个是他经过若干次撕纸后得到的碎纸片数 （ ）
A、2003 B、2004 C、2005 D、2006
9、一次函数y＝kx＋b的图象经过第一、二、四象限，则有 （ ）
A、k>0,b>0 B、k>0,b<0 C、k<0,b<0 D、k<0,b>0
10、已知数据：x1+3，x2+3，x3+3，x4+3的平均数是9，则数据x1，x2，x3，x4的平均数是 （ ）
A、5 B、6 C、7 D、8
二、填空题：（2＇×10＝20＇）
11、点A（1，－3）关于x轴对称的点B（ ），点A关于原点对称的点C（ ）。
12、写出一个一次函数的表达式 ，使它的图像经过点（0，3），且函数值随自变量的增大而减小。
13、小华用240元去购买单价为3元的一种商品，剩余的钱y（元）与购买这种商品的件数x（件）之间的函数关系是___________， x的取值范围是________．
14、如果点P（2，a）在函数y=2x－1的图象上，则点P的坐标为 .
15、地球的半径约为6.4×103km，它精确到 位，有 个有效数字。
16、计算：
；（
）（
）= 。
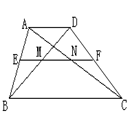
17、如图，梯形ABCD中，AD∥BC，中位线EF分别
交BD、AC于点M、N。若AD=4cm，EF=6cm，则
EM= cm，FN= cm，MN= cm，
BC= cm。
18、一组数据：35，43，25，43，37，28，42，29，30，数据的平均数是 ，
中位数是 。
19、已知一组数据：5，5，6，x，7，7，8的平均数是6，则这组数据的中位数是 ，众数是 。
20、若函数y=kx+b的图象平行于直线y=－2x，且经过点（3，－2）则此一次函数的表达式是 ．
三、解答题：
21、某种衬衫的进价是30元，当销售价是40元时，一天可以卖出60件。根据市场调查：销售价每降低1元，一天的销售量就增加5件。设销售价降低了x元,一天的销售量为y件。
（1）请写出y与x之间的函数关系式，自变量x的取值范围。(3’)
（2）当一天的销售量为80件时，总利润是多少？(2’)
22、如图，在正方形ABCD中，点E在边CD上，点F在边BC的延长线上，且CE=CF，则BE和DF有怎样的关系？为什么？(7’)
A
D
E
B C F
四、画图、计算：
23、用图像法解方程组：
(5’)
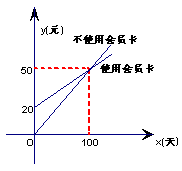24、某图书馆开展两种方式的租书业务:一是使用会卡,另一种是不使用会员卡.采用这两种方式,租书金额与租书时间之间的关系如图所示:
(1)分别写出不使用会员卡和使用会员卡租书的金额
(元) 与租书时间
(天)之间的函数关系式; (5’)
(2)若会员卡的使用期限是一年,则采用哪种方式比较划算? (2’)
25、已知等边三角形ABC边长为2，建立适当的直角坐标系，并写出点A、B、C的坐标。(6’)
A
B C
26、先观察下列等式，再回答问题：(4’)
①
②
③
（1）根据上面三个等式提供的信息，请猜想
的结果；
（2）请按照上面各等式反映的规律，试写出用
（为正整数）表示的等式。
27、某地举办乒乓球比赛的费用y（元）与参加比赛的人数x（人）是一次函数的关系。当x=20时y=1600；当x=30时y=2000。
⑴求y与x之间的函数关系式。 (4’)
⑵如果有50名运动员参加比赛，且全部费用由运动员分摊，那么每名运动员需要支付多少元？ (2’)
28、已知直线y=kx+b经过点A（2，0），与y轴交于点B，且S△AOB =4（O为原点），求这条直线的函数关系式。(8’)
29、如图：A、B是两个村庄，l是一条河流，且两村庄道河流的距离AC=1050米，BD=550，两村庄之间的水平距离CD=1300米，现在要在河边修建一个水泵站，分别向A、B两村庄送水，修在河边什么地方，可使所用的水管最短？
（１）画图找出水泵站的位置，用点Ｐ表示。(2’) A
（２）求水管最短是多少米？(4’)
B
C D l
30、下图是单位长度是1的网格： ⑴在图1中画出长度为
的线段AB；
⑵在图2中画出边长分别是
、
、4的三角形ABC；
⑶在图3中画出以格点为顶点面积为5的正方形. (6’)
 |