初二数学第一学期教学质量自查
(满分100分)
| 题次 | 一 | 二 | 三 | 四 | 合计 |
| 得分 |
同学们，祝贺你完成了一个阶段的学习，现在是展示你的学习成果之时，你可以尽情地发挥，祝你成功！
一、选择题（每小题3分，共15分）
1.下列计算正确的是( )
A．
B.
C.
D.
2.把不等式
的解集表示在数轴上,正确的是( )
 |
3.同学们都知道,国旗上的五角星(如图1)是是旋转对称图形,那么你知道
它需要旋转多少度后才能与自身重合?你的答案是( )
A.
B. 
C.
D.
4.如图2是一条线段AB,如果以A、B为基中两个顶点画位置 图1
不同的正方形，那么你一共可以画（ ）个.
Ａ．１ Ｂ．２ Ｃ．３ Ｄ．４
５．在做“抛掷两枚硬币实验”时，有部分同学没有硬币， A
B
因而需要选项用其它实物来替代进行实验，在以下所选 图2
用的替代物中，你认为较合适的是（ ）
A．两张扑克牌，一张红桃，一张黑桃. B．两个乒乓球,一个白色,一个黄色.
C．两个相同的矿泉水瓶盖. D．四张扑克牌,两张红桃,两张黑桃.
二、填空题(每小题目3分,共15分)
6.不等式
的解集是_____________.
7.计算:
=________________.
8.如图3,在矩形ABCD中对角线AC和BD的交点为O，
A
D
∠AOB=, AB=4cm, 则对角线AC=_______________。
9.如图4, DEF是由 ABC经过平移后得到的,平移
的距离是_________________. B C
图3
10.一个骰子,六个面上的数字分别为1、2、3、4、5、6，
投掷一次，向上的面出现数字1的机会是_____________. A D
三、解答题(每小题6分,共30分)
11.计算:
B E C F
图4
12.分解因式：
13.解不等式: 
,并把它的解集在数轴上表示出来.
14.如图5,画出用图中所示的图形绕O点逆时针方向旋转 
和
后所成的图形.
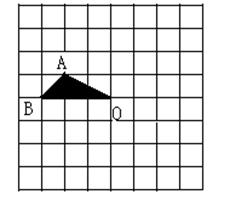
图5
15.已知:如图6, M是△ABC的中线BD上任一点,延长BD到N,使DN=DM..请判断四边形AMCN是什么四边形,并说明你的理由.
A
N
M D
B
C
图6
四、（每小题8分，共40分）
16．先化简，再求值：
，其中
.
17.在一次校运会上,老师将一堆羽毛球分给比赛小组,如果每组分3个,则还剩余8个;如果每组分5个,则最后一组得到的羽毛球少于3个.请问有几个比赛小组?
18.已知:如图7,在等腰梯形ABCD中,AB∥CD,AD=BC,AC为对角线,
AC平分∠DAB,AC ⊥BC.求 ∠DCA的度数.
D C
A
B
图7
19.如图8( a)是一种长为30cm,宽为20cm的矩形瓷砖,A、B、C、D分别为矩形各边的中点。现有一面长4.2m,宽2.8m的墙壁准备贴上瓷砖.如图8(b)是贴满瓷砖后的局部图.试问:
(1)这面墙壁至少要贴这种瓷砖多少块?
(2)全部贴满瓷砖后,其中有阴影的菱形有多少个?
D
|
|
B
图8（a）
图8（b）
20.下表是一个机器人做9999次“抛硬币”实验记录的结果:
| 抛掷次数 | 5 | 50 | 300 | 800 | 2000 | 3000 | 6000 | 8000 | 9999 |
| 出现正面的次数 | 1 | 30 | 135 | 408 | 988 | 1479 | 2980 | 3984 | 5006 |
| 出现正面的频率 | 20% | 51.0% | 49.4% | 49.8% | 50.1% |
(1)机器人抛掷50次和抛掷300次时所得正面的频率 之差是多少?抛掷3000次和抛掷6000次所得正面的频率之差又是多少?你从中发现了什么时候规律?
(2)根据表中数据绘制折线图?
(3)你能根据表中数据和折线图预测“抛掷硬币出现反面”这一事伯出现的机会均等有多大吗?
60%
|
50%
|
40%
|
30%
|
20%
|
10%
| |
 |
5 50 300 800 2000 3000 6000 8000 9999