初二数学第一学期期末试卷

初二数学第一学期期末试卷

出卷：洪澄　 考试时间：100分钟　满分100分

一、相信自己，把每题的唯一正确答案填入括号内（每小题3分，共21分）

1、下列运算中，错误的是（　　 ）

　 A．　 B．　 C．　 D．

2、如果直角三角形的三条边分别为1，4，a，那么a的值是（　）

　　A．　　  B．　　　 C．17或15　　 D．或

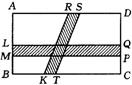
3、如图：矩形花园ABCD中，，，花园中建有一条矩形道路LMPQ 及一条平行四边形道路RSTK。若，则花园中可绿化部分的面积为 （　 ）　　

（A）　（B）

（C）　　（D）

4、老师给大家一个任务：从一张彩色纸中剪出一个正方形。

小明剪完后，这样检验它：他比较了边的长度，发现4条边都是相等的，小明觉得他完成了任务。 小兵用另一种方法检验：他量的不是边，而是对角线，发现对角线是相等的，小兵认为他也正确的剪出了正方形。　 小英剪完后，比较了由对角线互相分成的4条线段，发现它们都是相等的按照小英的意见，这说明剪出的四边形是正方形。你认为小明、小兵、小英三人中，正确的意见有（　）A.0种 B.1种 C.2种　D.3种

5、小明在设计一种平面（镶嵌）图案时，因不小心将墨水瓶打翻，把设计的部

分图案污染（如右图），则图中最下一行的图案（被墨水污染部分）应是（　 　）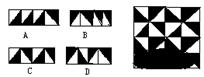

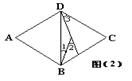
6、已知菱形ABCD，∠A=72°，将它分割成如图（2）所示的四个等腰三角形，则∠1，∠2，∠3，的度数分别是（　　）A、36°，54°，36°　　　 B、18°，54°，54°

C、18°，36°，36°　　D、54°，18°，72°

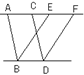
7、如图，AE∥BD， BE∥DF， AB∥CD，下面给出四个结论（1）AB=CD　（2）BE=DF

（3）S_ABDC=S_BDFE （4）S_△ABE=S_△DCF　 其中正确的有（　　）

 A、1个　　B、2个　 C、3个　　D、4个

二、能干的你一定可以把正确答案填入空格（每空2分）

1、的平方根是　　_，的算术平方根是　 ， 0.001的立方根是　　。

2、已知　　　　　　　　　 则　(x－y ) ² =　　　　  ,x²+y²=_______

3、△ABC的三边的长度分别为a、b、c ,且a、b满足＋b²－6b＋9＝0,则c的取值范围是____;

4、直角梯形ABCD中，∠A=∠B=90⁰，∠C=45⁰，AB=6cm,AD=2cm，则底边BC=_______，梯形ABCD的面积等于___________。

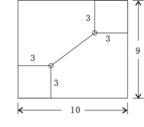
5、如图，工人师傅准备在一个长、宽分别是10cm，9cm的长方形铁板上打两个小孔，小孔的圆心距两边的距离都是3cm，则两孔圆心间的距离是　　 __cm。

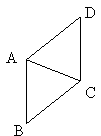6、如图，已知AC是菱形ABCD的一条对角线，且AC=CD，则∠BCD=　　度

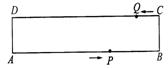7、如图,在矩形ABCD中, AB=20cm,BC=4cm,动点P从A开始沿AB边以每秒4cm的速度向B运动;动点Q从点C开始沿CD边以每秒1cm的速度向D运动,如果P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒。则(1)当t=1秒时,四边形APQD的面积是________㎝²(2)当t=_____秒时,四边形APQD为矩形。

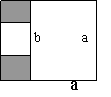
8、如图，长方形内有两个相邻的正方形，边长 分别为a和b，则阴影部分的面积为______.

9、给出一组式子：3²＋4²＝5²；8²＋6²＝10²；15²＋8²＝17²；24²＋10²＝26²，请你接着写出第五个式子：_____________________.

10、用一块面积为450cm²的等腰梯形彩纸做风筝，为了牢固起见，用竹条做梯形的对角线，对角线恰好互相垂直，那么至少需要竹条　　　　 cm．

三、沉着思考，冷静解答以下各题，

计算： （①②小题每题3分，③④每题4分，55分）

①(－2a²b)²·(－ab)÷(－b²)　　　　　　　 ② (x＋3)²－(x＋2)(x－2)

③若的值

④已知：，求：x+3y的平方根．

5做一做：

(1)观察下列各式：

　 　 　 ……

你发现了什幺规律？请你用含一个字母的等式将上面各式呈现的规律表示出来，试用你发现的规律填空：51²-49²=4×　　，75²-73²=4×　　 .　

(2)用所学数学知识说明你所写式子的正确性.　

四、实践与操作

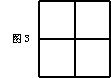
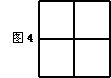
1、用四块如图l的瓷砖拼成一个正方形，请你在图2、图3、图4中各画出一种拼法，使图（2）是轴对称图形但不是中心对称图形，图（3）是中心对称图形但不是轴对称图形，图（4）既是轴对称图形又是中心对称图形(6分)

2、请阅读下列材料：（5分）

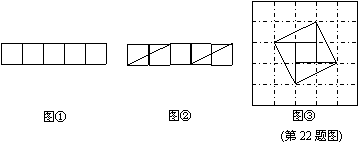
问题：现有5个边长为1的正方形，排列形式如图①，请把它们分割后拼接成一个新的正方形。要求：画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形。

小东同学的做法是：设新正方形的边长为x(x＞0)。依题意，割补前后图形的面积相等，有x²=5，解得x=。由此可知新正方形得边长等于两个小正方形组成得矩形对角线得长。于是，画出如图②所示的分割线，拼出如图③所示的新正方形。

请你参考小东同学的做法，解决如下问题：

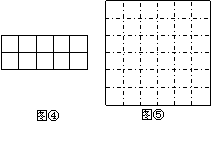
现有10个边长为1的正方形，排列形式如图④，请把它们分割后拼接成一个新的正方形。要求：在图④中画出分割线，并在图⑤的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形。

说明：直接画出图形，不要求写分析过程。

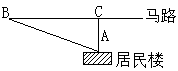
五、如图，居民楼与马路是平行的，相距9m，在距离载重汽车41m处就可受到噪声影响，试求在马路上以4m/s速度行驶的载重汽车，给一楼的居民带来多长时间的噪音影响？若时间超过25秒，则此路禁止该车通行，你认为载重汽车可以在这条路上通行吗？（5分）

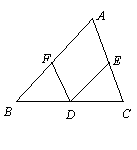
六、如图，在△中，为边的中点，E是AC中点，F是AB中点.（7分）

（1）证明：△≌△ ；

（2）如果给△添加一个条件，使四边形成为菱形，则该条是　　 ；

如果给△添加一个条件，使四边形成为矩形，则该条件是　　　　.

（均不再增添辅助线） 请选择一个结论进行证明.

七、我们给出如下定义：若一个四边形的两条对角线相等，则称这个四边形为等对角线四边形。请解答下列问题：（7分）

（1）写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称；

（2）探究：当等对角线四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和与其中一条对角线的大小关系，并证明你的结论。