八年级数学第一学期学区期中考试
试题卷
温馨提示：同学们考试就要开始了，请不要粗心，要注意把握考试时间，努力吧！
一、选择题：（每题3分，共30分）
1、将下列长度的三根木棒首尾顺次连接，能组成直角三角形的是………………（ ）．
（A）1、2、3 （B）2、3、4 C）3、4、5 （D）4、5、6
2、已知∠1和∠2是同位角，∠1=40°，∠2等于（ ）
A、160° B、140° C、40° D、无法确定
3、下列各图中，不可能折成无盖的长方体的是（ ）
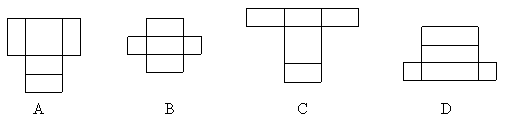
4、、下列说法正确的是-------------------------（ ）
A. 顶角相等的的两个等腰三角形全等
B. 等腰三角形的中线、高互相重合
C. 在同一个三角形中，有两个底角相等的三角形是等腰三角形
D. 有两个角互余的三角形是直角三角形
5、直角三角形两直角边长为5和12，则此直角三角形斜边上的中线的长是（ ）
A、5 B、6 C、6.5 D、13
6、如果一个等腰三角形的一个角为30º，则这个三角形的顶角为（ ）
A、120º B、30º C、120º或30º D、90º
7、下列各项调查中，比较适合采用普查的是（ ）
A、审查书稿的科学性 B、调查某种子弹的威力
C、在全国范围内调查新教材的使用情况 Ｄ、在某林区内调查野鹿的数目
8、某青年排球队12名队员年龄情况如下：
| 年龄 | 18 | 19 | 20 | 21 | 22 |
| 人数 | 1 | 4 | 3 | 2 | 2 |
则这12名队员年龄的众数、中位数分别是（ ）
（A）20，19 （B）19，20 （C）19，20.5 （D）19，19
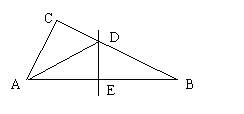9、如图，△ABC中，∠C=90°，AB的中垂线DE交AB于E，交BC于D，若AB=10，AC=6，则△ACD的周长为（ ）
A、16 B、14 C、20 D、18 、
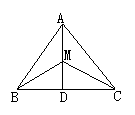10、如图所示，已知△ABC中，AB=6，AC=9，AD⊥BC于D，M为AD上任一点，则 MC2-MB2等于（ ）
（A）9 （B）35 （C）45 （D）无法计算
二、填空题：（每小题3分，共30分）
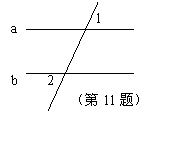
11、如图，若a∥b，∠1=40°，则∠2= 度；
12、已知一个等腰三角形的两边长分别是3和7，那么这个等腰三角形的周长为 ；
13、有一块田地的形状和尺寸如图所示，则它的面积为 。
 | |||
 | |||
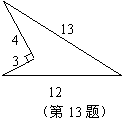14、为了让人们感受丢弃塑料袋对环境造成的影响，某班环保小组的六名同学记录了自已家中一周内丢弃的塑料袋的数量，结果如下(单位：个)：33,25,28,26,25,31，如果该班有45名学生，那么根据提供的数据估计该周全班同学各家总共丢弃塑料袋的数量约为 。
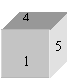
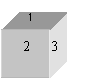
15、一个骰子由1-6这6个数字组成，请你根据下图中的三种状态里所显示的数字，推出“？”处的数字是-------------------------。。
 |  |  | |||
16、已知一组数据x1，x2，x3，x4，x5 的方差为3，则另一组新数据2x1+5，2x2+5，2x3+5，2x4+5，2x5+5的方差为 。
17、已知等腰三角形一腰上的中线将它周长分成18cm和12cm 两部分，则这个等腰三角形的底边长是＿＿＿＿＿＿。
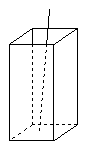
18、如图，将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和10
㎝的长方体无盖盒子中，则细木棒露在盒外面的最短长度是 ㎝．
19、如图，把矩形ABCD沿EF折叠，使点C落在点A处，点D落在点G处，若∠CFE=
，且DE=1，则边BC的长为
3 ．
20、如图，在一个正方形被分成三十六个面积均为1 的小正方形，点A与点B在两个格点上，问在格点上是否存在一个点C，使△ABC的面积为2，这样的点有 个。
 |
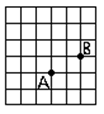
三、解答题：（共7小题，共40分）
21、作图题：（5分）相同的小正方形搭成的几何体如图所示，请画出它的三视图。
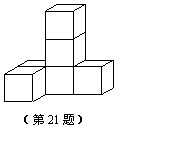
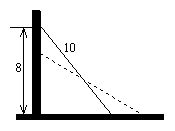22、（5分）如果一个长为10m的梯子，斜靠在墙上，梯子的顶端距地面的垂直距离为8m．如果梯子的顶端下滑1m，请猜测梯子底端滑动的距离是否会超过1m，并加以说明．
23、如图，AD是等腰三角形ABC的底边BC上的高，DE∥AB，交AC于点E，判断△ADE是不是等腰三角形，并说明理由。（5分）
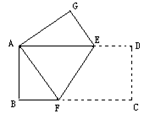
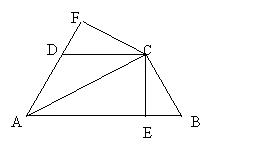
24、（5分）如图所示，已知：AB=BC=AC，CD=DE=EC，求证：AD=BE．
25、（7分）如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD，
（1）求证：△BCE≌△DCF; （3分）
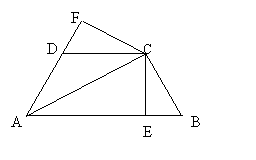（2）若AB=21，AD=9，BC=CD=10，求AC的长。 （4分）
26、（6分）某校拟派一名跳高运动员参加一项校际比赛，对甲、乙两名跳高运动员进行了8次选拔比赛，他们的成绩（单位：米）如下：
甲：1.70 1.65 1.68 1.69 1.72 1.73 1.68 1.67
乙：1.60 1.73 1.72 1.61 1.62 1.71 1.70 1.75
（1） 要评价这2位运动员的平均水平，你选择什么统计量？求出这个统计量。
（2） 请求出两组数据的方差，这两个方差的大小反映了什么？
（3） 经预测，跳高1.65米就很难获得冠军，该校为了获取跳高比赛冠军，可能选哪位运动员比赛？若预测跳高1.70米方获得冠军呢？
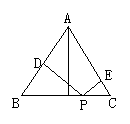
27、（7分）已知等边△ABC和点P，设点P到△ABC三边的AB、AC、BC的距离分别是h1，h2，h3，△ABC的高为h，请你探索以下问题：
(1)若点P在一边BC上（图1），此时h1、h2、h3与h之间有怎样的关系 ，
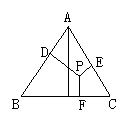
(2)若当点P在△ABC内（图2）,此时h1、h2、h3与h之间有怎样的关系
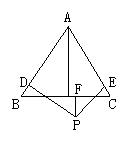
(3)若点P在△ABC外（图3），此时h1、h2、h3与h之间有怎样的关系 ，请写出你的猜想，并选一种情况说明理由．
(1) (2) (3)
温馨提示：考完了吗？请重新认真地检查一遍，预祝你考出好成绩！
第一学期学区期中考试
八年级数学参考答案
一、选择题（共10小题，3分×10＝30分）
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| C | D | A | D | C | C | A | B | B | C |
二、填空题（共8小题，3分×10＝30分）
11、 40º ． 12、 17 ． 13、 24 .
14、 1260个 ． 15、 6 ． 16、 12 ．
17、 6cm或14cm ． 18、 5 . 19、 3 ．
20、 5 ．
| |
三、解答题（共7小题，5分＋5分＋5分＋5分＋7分＋6分＋7分＝40分）
21、略
22、超过1m，
-6>7-6=1
23、解：△ADE是等腰三角形，理由如下：
∵AD是等腰三角形ABC的底边BC上的高，
∴∠BAD=∠CAD（等腰三角形三线合一定理）
∵DE∥AB
∴∠BAD=∠ADE（两直线平行，内错角相等）
∴∠CAD=∠ADE
∴△ADE是等腰三角形
24、略
25、解：（1）（3分）∵AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，
∴∠CFD=90°，∠CEB=90°（垂线的意义）
CE=CF （角平分线的性质）
∵BC=CD （已知）
∴Rt△BCE≌Rt△DCF （HL）
（2）（4分） 由（1）得，
Rt△BCE≌Rt△DCF
∴DF=EB 设DF=EB=X
∵∠CFD=90°，∠CEB=90°，
CE=CF，AC=AC
∴Rt△AFC≌Rt△AEC （HL）
∴AF=AE
即：AD+DF=AB－BE
∵AB=21，AD=9，DF=EB=x
∴9+x=21－x 解得，x=6
在Rt△DCF中，∵DF=6，CD=10
∴CF=8
∴Rt△AFC中，AC2=CF2+AF2=82+（9+6）2=289
∴AC=17
答：AC的长为17。
26、（1）平均数 甲平均数：1.69。乙平均数：1.68。
（2）甲方差为0.0006，乙方差为0.00315，甲方差<乙方差，甲成绩稳定
（3）跳高1.65米就很难获得冠军，则会选甲运动员，因为在8次比赛中甲运动员有7次达到1.65米以上，乙运动员只有5次达到1.65米以上；若预测跳高1.70米方获得冠军，则会选乙运动员，因为在8次比赛中甲运动员只有3次达到1.70米，乙运动员有5次达到1.70米；
27、图1，2：h1+h2+h3=h；图3：h1+h2+h3>h且h1+h2-h3=h．提示：利用面积．