八年级数学期中试卷(上)
一、填空（本大题共10小题，每题3分，共30分）
1、下列函数（1）y=πx (2)y=2x-1
(3)y= (4)
(5)y=x2-1
中，是一次函数的是： （填序号）。
2、将函数y＝２x＋４的图象向下平移３个单位，所得函数的解析式为 。
3、对某班同学的身高进行统计(单位:厘米),频数分布表中165.5～170.5这一组学生人数是12,频率为0.25,则该班共有 名同学。
4、若点（a,b）在第四象限，则直线y＝aX+b不经过第 象限。
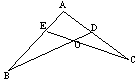5、如图所示根据SAS，如果AB=AC， = ，
即可判定ΔABD≌ΔACE。
6、某种储蓄的月利率为0.2％，存入100元本金，则本息和y（元）与所存月数x之间的函数关系为 。
7、如果直线y=3x+b与y轴交点的纵坐标为-2，那么这条直线一定不经过第 象限。
8、若一次函数y=（1-2m）x+m的图象经过点A(x1,y1),B(x2,y2),
当x1＜x2时y1＞y2，则m的取值范围是 。
9、如图在ΔABC中，AD=AE，BD=EC，∠ADB=∠AEC=105°，
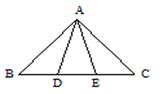∠B=40°，则∠CAE= 。
（第10题图） （第9题图）
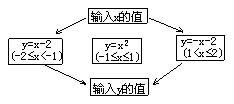
10、根据上图所示的程序计算函数值，
若输入x的值为
，则输出的结果为 。
二、选择（本大题共6小题，每题3分，共18分）
11、下列函数中，y随x的增大而减小的有（ ）。
①
②
③
④
A、1个 B、2个 C、3个 D、4个
12、对某班４０名学生的一次数学测试成绩进行统计，频数分布表中８０≤x＜９０这一组的频率为０．２，那么这４０名学生的数学成绩在８０≤x＜９０这个分数段的人数是（ ）。
A、２０ B、１０ C、８ D、１２
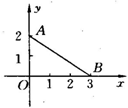13、 如图，线段AB对应的函数表达式为（ ）
A、y=-x+2
B、y=-
x+2
C、y=-x+2（0≤x≤3） D、y=-x+2（0<x<3）
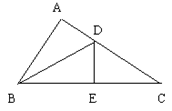14、如图在DABC中，D、E分别是AC、BC上的点，若DADB≌DEDB≌DEDC，则∠C的度数为（ ）
A、30° B、25°
C、20° D、15°
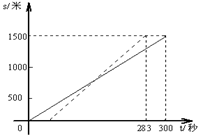15、甲、乙两人在一次赛跑中，路程s（米）与时间t（秒）的关系如图所示（实线为甲的路程与时间的关系图象，虚线为乙的路程与时间的关系 图象），小明根据图象得到如下四个信息，其中错误的是（ ）
A、这是一次1500米的赛跑
B、甲、乙同时起跑
C、甲、乙两人先到达终点的是乙
D、甲在这次赛跑中的速度是5米/秒 16、在△ABC和△A＇B＇C＇中，①AB=A＇B＇ ②BC=B＇C＇，③CA=C＇A＇④∠A=∠A＇ ⑤∠B=∠B＇ ⑥∠C=∠C＇，则下列各组条件中能判定两个三角形全等的是（ ）。
A、 ①②④ B、 ②④⑥ C 、④⑤⑥ D、 ②③⑤
三、（本大题共3小题，第17小题6分，第18、19小题每题7分，共20分）
17、如图：已知AB⊥BC,AD⊥DC,∠1=∠2,垂足分别为B、D。
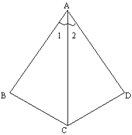求证：AB=AD
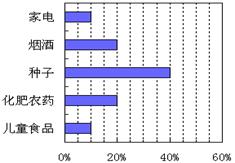18、消费者协会在3月15日消费者权益日来临之际，对一周内收到的投诉电话作了统计，如图所示。其中接到关于种子的投诉电话最多，共70个，请就下列问题予以解答：
〈1〉本周共接到多少个投诉电话？
〈2〉有关化肥农药的电话有多少个？
〈3〉请就上图提供的信息提一些建议。
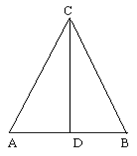19、如图小明是这样验证旗杆是否垂直，他先在西侧选取一点A，再在东侧选取一点B，使旗杆的底部D与A、B在同一条直线上，并且AD=BD，然后将旗杆从旗杆顶部C拉至A、B，只要绳子CA=CB，即知道旗杆CD是和地面垂直的。请你说说这是什么道理。
四、(本大题共３小题，每题８分，共２４分)
20、为发展电信事业，方便用户，电信公司对移动电话采用不同的收费方式。其中，使用的“便民卡”与“如意卡”，在某市范围内每月（３０天）的通话时间x（分）与通话费y（元）的关系如图所示。
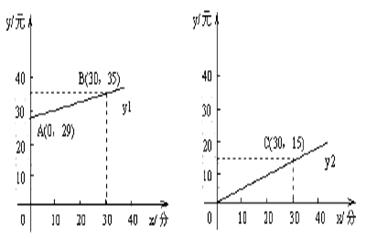〈1〉分别求出通话费用y
（用便民卡）、y
（用如意卡）与通话时间x之间的函数关系式；
〈2〉请帮助用户计算一下，在一个月内使用哪种卡便宜？
21、已知一次函数y=（４m＋1）x－(m＋1)求：（１）m为何值时，y随x的增大而减小？（２）m为何值时，此直线与y轴交点在x轴的下方？（３）m为何值时，此直线不过第三象限？
22、已知一次函数的图象经过点A（-3，4）、B（-1，-2）。
〈1〉求出这个一次函数的解析式，并画出图象。
〈2〉求ΔAOB的面积。
五、（本大题共2小题，每小题9分，共18分）
| 分组 | 频数累计 | 频数 | 频率 |
| 0.55～1.05 | 正正 | 14 | 0.28 |
| 1.05～1.55 | 正正正 | 15 | 0.30 |
| 1.55～2.05 | 正 | 7 | |
| 2.05～2.55 |
| 4 | 0.08 |
| 2.55～3.05 | 正 | 5 | 0.10 |
| 3.05～3.55 | 3 | ||
| 3.55～4.05 |
| 0.04 | |
| 合计 | 50 | 50 | 1.00 |
23、为了了解学校开展“孝敬父母，从家务做起”活动的实施情况。该校抽取初二年级50名学生，调查他们一周（按七天计算）做家务所用的时间（单位：小时），得到一组数据，并绘制成下表。请根据该表回答下列各题：
〈1〉将频数分布表补充完整。
〈2〉由以上信息判断，每周做家务的时间不超过1.5小时的学生所占的百分比。〈3〉作出反映调查结果的统计图。
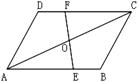24、如图，AB=CD，AD=BC，EF经过AC的中点O，分别交AB、CD于E、F。 求证：OE=OF.
六、（本大题共１小题，共１０分）
25、⑴已知：如图1，点C为线段AB上一点，△ACM，△CBN是等边三角形，求证：AN=BM，这时可以证明 ____________，得到AN=BM. （3分）
⑵如果去掉“点C为线段AB上一点”的条件,而是让△CBN绕点C旋转成图2的情形,还有“AN=BM”的结论吗?如果有,请给予证明.（7分）
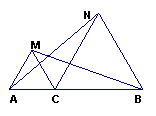
图1 图2