八年级秋期中考试数学试题
（总分100分，90分钟完卷）
一、选择题：（每题3分，共30分）
1、一次函数y=－2x+3，则函数不经过的象限是（ ）
A、一象限 B、二象限 C、三象限 D、四象限
2、下列函数是一次函数的是（ ）
A、y=x3 B、y=2x2＋1 C、y=
D、 y=－3x
3、李明骑车上学，一开始以某一速度行进，途中车子发生故障，只好停下来修车，车修好后，因怕迟到，于是加快了骑车的速度，在以下给出的四个函数图象中（S是距离，t是时间），符合以上情况的是（ ）
 |  |  |  |
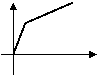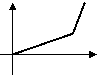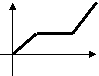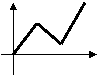A B C D
4、汽车由天津开往相距120km的北京，若它的平均速度为60km/h，则汽车距北京的路程s（km）与行驶时间t（h）之间的函数关系式是（ ）
A、s=60t B、s=120-60t C、s=（120-60）t D、s=120+60t
5、一次函数y=kx-k的图像大致是（ ）
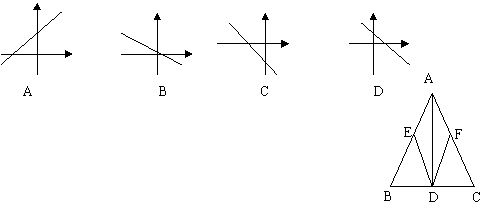
6、已知等边△ABC，AD是高线，∠EDB=∠FDC=60º，
则与BD相等的边有（ ）条
A、二条 B、三条 C、四条 D、五条
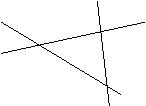7、如图，三条直线表示三条相互交叉的公路，现要建一个货
物中转站，要求它到三条公路的距离相等，则可供
选择的地址有（ ）
A．1处 B.2处 C.3处 D.4处
8、小明站在镜子前，他在镜子中的像只举起了右手，则小明实际上举手的情况是（ ）
A、举起了左手 B、举起了右手
C、左手与右手都举了 D、两只手都没举
9、如图所示，已知∠A=∠D ，CD=AF，那知要得到△ABC≌△DEF，
给出的条件中可以使用的条件有（ ）个。
（1）DE=AB （2）EF=BC （3）∠E=∠B（4）BC∥EF
A、1个 B、2个 C、3个 D、4个
10、O为锐角△ABC的∠C平分线上一点,O关于AC、BC的对称点分别为P、Q,则△POQ一定是( )
A、等边三角形 B、等腰三角形 C、直角三角形 D、等腰直角三角形
二、填空题：（每空3分，共24分）
11、函数
中，自变量x的取值范围是________________.
12、函数y=2x-4与两坐标轴围成的三角形的面积为 。
13、已知梯形的上底长为x，下底长为15，高为8。
（1）梯形面积y与上底长x之间的函数关系为 ；
（2）当x=10时，y= 。
14、函数y=(2m－1)x＋3的图象经过点（x1,y1）和（x2,y2）,且x1＜x2，y1＞y2，求m的取值范围是 。
15、在黑体的汉字“口天日”等是轴对称图形，请再写出三个这样的汉字。______________
16、如图，长方形ABCD沿AE折叠使点D落在BC边上的F点处，如果∠BAF=60º，
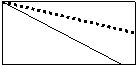则∠DAE的度数是
17、已知一次函数图象经过点（3，5）和（－4，－9）
两点，则这个一次函数的解析式是 。
三、解答题：（共46分）
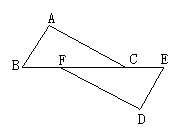
18、（6分）如图，点B，F，C，E在一条直线上，
FB=CE，AB∥ED，AC∥FD。求证：AB=DE
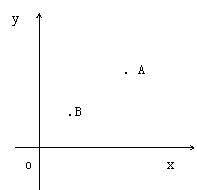
19、（6分）如图，村庄A和村庄B位于一条河流的同侧，以河流为x轴建立如图所示的坐标系.两地的坐标分别为A（5，8），B（2，1）.现要在河边修建一水泵站分别向两地供水，那么泵站建在何处，能使供水管道总长最短？（画出图形，并指出水泵站的坐标）.
 |
20、（6分)如图，是一位护士统计一位病人 的体温变化图：根据统计图回答下列问题：
⑴病人的最高体温是达多少？
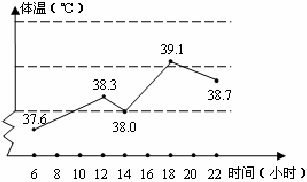
⑵什么时间体温升得最快？
⑶如果你是护士，你想对病人说:
_________________________________________.
21、（7分）如图ΔABC中，AB=AC，点D在AC上，且AD=BD=BC。
求ΔABC各角的度数。
22、（7分）Ａ城有肥料300吨，Ｂ城有肥料200吨，现要把这些肥料全部运往Ｃ、Ｄ两乡．从
Ａ城往Ｃ、Ｄ两乡运肥料费用分别为每吨20元和25元；从Ｂ城往Ｃ、Ｄ两乡运肥料费用分
别为每吨15元和24元．现Ｃ乡需要肥料240吨，Ｄ乡需要肥料260吨．怎样调运总运费最少？
23、（7分）、等腰三角形的周长为20cm，底边长为ycm,腰长为xcm 。
（1） 写出y关于x的函数关系式；
（2） 腰长x可以为5吗？如果能，请求出底边长y；若不能，请说明理由。
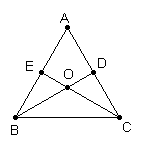24、（7分）如图所示，在ΔABC中，D、E分别是AC、AB上的点，
BD与CE相交于O点，现给出下列四个条件：①∠EBO=∠DCO；
②∠BEO=∠CDO；③BE=CD；④OB=OC；
（1）上述四个条件中，能用其中两个条件判定ΔABC是等腰三角形吗？（用序号写出所有可能的情况）；
（2）选择（1）中的任意一种情况进行证明。