八年级上册数学期中测试卷
班级________学号________姓名________成绩________
一、选择题(每小题4分,共48分)
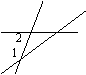
1.如图,直线a,b被直线c所截,如果a∥b,∠1=50°,那么∠2的度数为 ( )
A.40° B.80° C.100° D.130°’
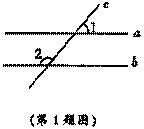
2、下列各图中,∠1与∠2是同位角的是( )
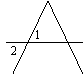
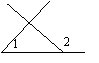
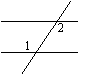
 |
A B C D
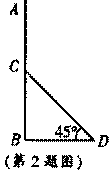
3.如图,电线杆AB的中点C处有一标志物,在地面D处测得标志物的仰角∠CDB=45°,如果点D到电线杆底部点B的距离为a,那么电线杆AB的长可表示为( )
A. a B. 2a C. 3a D.不确定
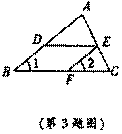
4.如图,在△ABC中,D,E,F分别在AB,AC,BC上,且EF∥AB,要使DE∥BC,只需再满足下列条件中的 ( )
A.∠1=∠2 B.∠1=∠DEF C.∠1=∠ADE D.∠2=∠AED
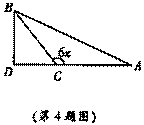
5.如图,在Rt△ADB中,∠D=90°,C为AD上一点,那么x可能是 ( )
A.20° B.30° C.40° D.50°
6.一个直棱柱的底面和侧面的形状、大小一样,这个直棱柱是 ( )
A直三棱柱 B.直四棱柱 C.直五棱柱 D.直六棱柱
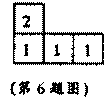
7.图甲是由几个小立方块所搭几何体的俯视图,小正方形中的数字表示在该位置的小
立方块的个数,这个几何体的主视图是下列各图中的 ( )
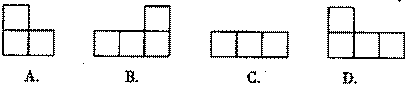
8.一个立方体的表面展开图如图所示,将其折叠为立方体后的立体图形是( )

9,为了了解本地区老年人一年中生病的次数,下列收集数据的方式最合理的是 ( )
A到公园里调查1000名晨练老人 B.到医院调查1000名老年病人
C.调查10名老年邻居;D.利用派出所户籍资料,按抽样规则抽查本地区10%的老年人
10.巳知甲、乙两组数据的平均数相等,且甲组数据的方差S2甲=0.55,乙组数据的方差S2乙=0.15,那么 ( )
A甲组数据比乙组数据波动大 B.乙组数据比甲组数据波动大
C甲组数据与乙组数据的波动一样大 D.甲、乙两组数据的数据波动不能比较
11.已知一组数据3,7,9,10,x,12的众数是9,那么这组数据的中位数是( )
A.3 B.9 C.9.5 D. 12
12.已知等腰三角形ABC的底边BC=8cm,且AC-BC=2cm,那么腰AC的长为( )
A.10cm或6cm B.10cm C.6cm D.8cm或6cm
二、填空题(每小题5分,共30分)
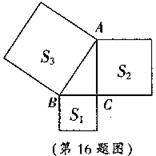
13如图,以Rt△ABC的三边为边镶外作正方形,其面积分别为S1,S2,S3,且S1=4,S2=8,那么S3=_______。
14.直角三角形斜边上的中线长为2cm,一条直角边长为cm,那么这个直角三角形的另一条直角边长为______cm。
 子
子 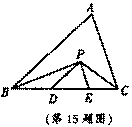
15.如图,在△ABC中,BC=5cm,BP,CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC那么△PDE的周长是______cm.
16.如果一个直四棱柱的底面是边长为2cm的正方形,侧棱长为4cm,那么这个直四棱柱的体积为______cm。
17.刚刚喜迁新居的小华同学为估计今年六月份的家庭用电量,在六月上旬连续7天同一时刻观察电表显示的度数并记录如下:
| 日 期 | 1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 |
| 电表显示数(度) | 24 | 27 | 31 | 35 | 42 | 45 | 48 |
请你预计小华同学家六月份用电总量约是______度。
18、已知一个样本:1,2,3,4,5,那么这个样本的标准差是__________。
三、解答题(共72分)
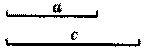
19.(8分)已知线段a,c(如图),用直尺和圆规作Rt△ABC,使∠C=Rt∠,BC=a,AB=c。(保留作图痕迹,不写作法)
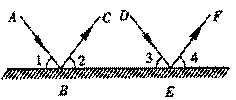
20.(8分)如图,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4。
(1)∠1,∠3的大小有什么关系?∠2与∠4呢?
(2)反射光线BC与EF也平行吗?为什么?
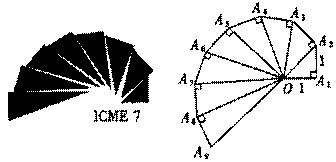
21.(8分)下图是第七届国际数学教育大会的会徽.它的主题图案是由一连串如图所示的直角三角形演化而成的.设其中的第一个直角三角形OA1A2是等腰三角形,且OA1=A1A2=A2A3=A3A4=……=A8A9=1,请你计算图中其它8条线段的长,并填在下面的表格中。
| OA2 | OA3 | OA4 | OA5 | OA6 | OA7 | OA8 | OA9 |
|
|
|
|
|
|
|
|
|
22.(9分)由相同小立方体搭成的几何体如图所示,画出这个几何体的三视图.
23.(12分)某校拟派一名跳高运动员参加一项校际比赛,对甲、乙两名跳高运动员进行了8次选拔比赛,他们的成绩(单位:米)如下:
甲:1.70 1.65 1.68 1.69 1.72 1.73 1.68 1.67
乙:1.60 1.73 1.72 1.61 1.62 1.71 1.70 1.75
(1)要评价这2位运动员的平均水平,你选择什么统计量?求出这个统计量。
(2)请求出两组数据的方差,这两个方差的大小反映了什么?
(3)经预测,跳高1.65米就很肯获得冠军,该校为了获取跳高比赛冠军,可能选哪位运动员比赛?若预测跳高1.70米方获得冠军呢?
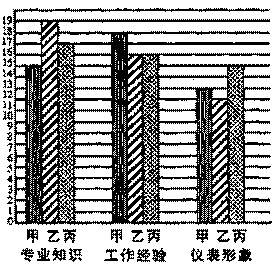
24.(13分)春兰集团对应聘者甲、乙、丙进行面试,并从专业知识、工作经验、仪表形象三方面给应聘者打分,每一方面满分20分,最后的打分制成条形统计图(如图).
(1)利用图中提供的信息,在专业知识方面3人得分的平均数是多少?在工作经验方面3人得分的众数是多少?在仪表形象方面谁最有优势?
(2)如果专业知识、工作经验、仪表形象三个方面的重要性之比为10∶7∶3,那么作为人事主管,你应该录用哪一位应聘者?为什么?
(3)在(2)的条件下,你对落聘者有何建议?
25.(14分)已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,O是AB的中点,E,F分别在AC,BC上,且ED⊥AC.FD⊥BC
(1)说出AD=DC=DB的理由; (2)DE,DF是否相等?请说明理由;
(3)如果AB=10cm,求四边形CEDF的面积。