等腰三角形练习题
班级 姓名 学号
一.填空题
1.等腰三角形的腰长是底边的![]() ,底边等于12cm,则三角形的周长为 cm
,底边等于12cm,则三角形的周长为 cm
2.等腰三角形顶角为80°,则一腰上的高与底边所夹的角的度数为____度
3.等腰三角形的底角是65°,顶角为________.
4.等腰三角形的一个内角为100°,则它的其余各角的度数分别为_______.
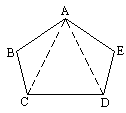
5. P为等边△ABC所在平面上一点,且△PAB,△PBC,△PCA都是等腰三角形,这样的点P有_______个.
6. 等腰三角形的顶角等于一个底角的4倍时, 则顶角为_________度.
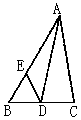
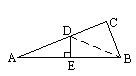
7. 已知如图,A、D、C在一条直线上AB=BD=CD, ∠C=40°,则∠ABD=_ 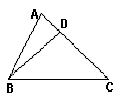
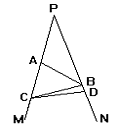
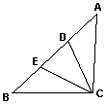
第7题 第9题 第10题
8. 在等腰△ABC中, AB=AC, AD⊥BC于D, 且AB+AC+BC=50cm,
而AB+BD+AD=40cm, 则AD=___________cm.
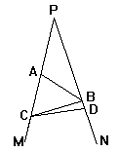
9. 如图, ∠P=25°, 又PA=AB=BC=CD, 则∠DCM=_______度.
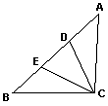
10. 如图已知∠ACB=90°, BD=BC, AE=AC, 则∠DCE=__________度.
二.单选题
1. 等腰三角形一底角为30°,底边上的高为9cm,则腰长为___cm.[ ]
![]()
2. 不满足△ABC是等腰三角形的条件是[ ]
A.∠A:∠B:∠C=2:2:1 B.∠A:∠B:∠C=1:2:5
C.∠A:∠B:∠C=1:1:2 D.∠A:∠B:∠C=1:2:2
3. 等腰三角形的一个角等于20°, 则它的另外两个角等于:[ ]
A.20°、140°B.20°、140°或80°、80°C.80°、80° D.20°、80°
4. 下列命题正确的是[ ]
A.等腰三角形只有一条对称轴 B.直线不是轴对称图形
C.直角三角形都不是轴对称图形 D.任何一角都是轴对称图形
5. 等腰三角形一腰上的高与底所夹的角等于 [ ]
A.顶角 B.顶角的![]() C.顶角的2倍 D底角的
C.顶角的2倍 D底角的![]()
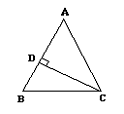
7. 如图, 在△ABC中, AB=AC, CD⊥AB于D, 则下列判断正确的是[ ]
A.∠A=∠B B.∠A=∠ACD C.∠A=∠DCB D.∠A=2∠BCD
第7题 第10题
8. 等腰三角形两边分别为35厘米和22厘米, 则它的第三边长为[ ]
A.35cm B.22cm C.35cm或22cm D.15cm
9. 等腰三角形中, AB长是BC长2倍, 三角形的周长是40, 则AB的长为[ ]
A.20 B.16 C.20或16 D.18
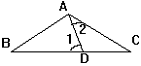
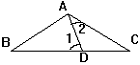
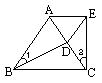
10. 如图已知: AB=AC=BD, 那么∠1与∠2之间的关系满足[ ]
A.∠1=2∠2 B.2∠1+∠2=180°
C.∠1+3∠2=180° D.3∠1-∠2=180°
三.证明题
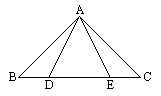
1. 如图, 已知:点D,E在△ABC的边BC上,AB=AC,AD=AE.求证:BD=CE
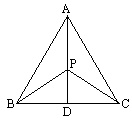
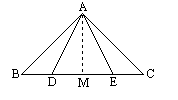
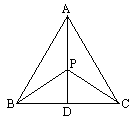
2. 如图:△ABC中,AB=AC,PB=PC.求证:AD⊥BC
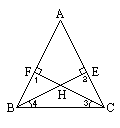
3. 已知:如图,BE和CF是△ABC的高线,BE=CF,H是CF、BE的交点.
求证:HB=HC
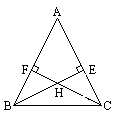
4. 如图,在△ABC中,AB=AC,E为CA延长线上一点,ED⊥BC于D交AB于F.
求证:△AEF为等腰三角形.
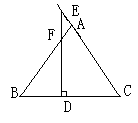
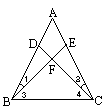
5. 如图,△ABC中,D在BC延长线上,且AC=CD,CE是△ACD的中线,CF平分
∠ACB,交AB于F,求证:(1)CE⊥CF;(2)CF∥AD.
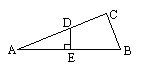
6.如图:Rt△ABC中,∠C=90°,∠A=22.5°,DC=BC, DE⊥AB.求证:AE=BE.
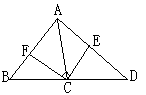
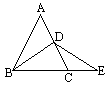
7.已知:如图,△BDE是等边三角形,A在BE延长线上,C在BD的延长线上,且AD=AC。求证:DE+DC=AE。
等腰三角形练习题答案
一.填空题
1. 30 2. 40 3. 50° 4. 40°40° 5. 7
6. 120 7. 20 8. 15 9. 100 10. 45
二.单选题
1. B 2. B 3. B 4. D 5. B 6. A
7. D 8. C 9. B 10. D
三.证明题
1. 证:作AM⊥BC于M
∵AD=AE,∴DM=EM
∵AB=AC,∴BM=CM
∴BM-DM=CM-EM
∴BD=CE
2. 证明:
在△ABP和△ACP中
∵AB=AC,BP=PC,AP=AP
∴△ABP≌△ACP (SSS)
∴∠BAP=∠CAP
∴AD⊥BC(等腰三角形顶角平分线又是底边的垂线)
3. 证明:∵△ABC是等边三角形
∴AB=AC,∠BAC=60°
在△ABD和△ACE中
∵AB=AC,∠1=∠2,BD=CE
∴△ABD≌△ACE (SAS)
∴AD=AE,∠BAD=∠CAE=60°
∴在△ADE中
∵AD=AE,∠DAE=60°
∴△ADE为等边三角形.
4. 证明:
连结AC和AD
在△ABC和△AED中
AB=AE BC=ED ∠B=∠E
∴△ABC≌△AED (SAS)
∴∠ACB=∠ADE,AC=AD
∴ △ACD是等腰三角形
∴∠ACD=∠ADC;∠BCA=∠CDE
∴∠C=∠D
5. 证明:∵BE、CF是△ABC的高线.
∴∠1=∠2=90°
∴△BCF和△CBE都是Rt△.
在Rt△BCF和Rt△CBE中
∵CF=BE,BC=CB
∴Rt△BCF≌Rt△CBE
∴∠3=∠4
在△HBC中 ∵∠3=∠4
∴HB=HC(同一三角形中,等角对等边)
6. 证明:∵AE=AD,∠1=∠2,∠A公共角
∴△AEF≌△ADC (AAS)
∴AB=AC,EB=DC
∴∠ABC=∠ACB
∴∠3=∠4,BF=CF
∴DF=EF
7. 证明:∵AB=AC
∴∠B=∠C
∵ED⊥BC
∴∠B+∠BFD=∠B+∠EFA=90°∠C+∠E=90°
∴∠E=∠EFA
∴AE=AF
8. 证明:(1)∵AC=CD,CE是△ACD的中线
∴∠ACE=∠DCE 又∵CF平分∠ACB
∴∠ACF=∠BCF ∴∠AFC=∠AEC=90°
∴CE⊥CF
(2)∵AC=CD,CE是△ACD的中线
∴CE⊥AD ∴CF∥AD
四.证明题(本题包括4小题,共24分。)
1. 证明:∵△ABC是等边三角形,BD是中线.
∴BD⊥AC,∠CBD=30°,∠BCD=60°
∵DC=CE ∴∠E=∠CDE=30°
∴∠CBD=∠E,∴ DB=DE
2. 证明:连结DB
∵∠CDB为△ADB外角,∴∠CDB=∠A+∠DBA
∵△CDE中,DC=BC,∴∠CDB=∠CBD=∠A+∠DBA
∵△ABC中,∠C=90°,∴∠A+∠DBA+∠CBD=90°
∴∠A+∠DBA=45°
∵∠A=22.5°∴∠DBA=45°-22.5°=22.5°=∠A
∴△DAB中,AD=DB
∴△DAB为等腰三角形
∵△DAE中,DE⊥AB于E,∴DE为△ADB中AB边中线
∴E为AB中点,∴AE=EB
3. ![]()
4. ![]()
![]()
-----------------------------------------------
试题备注
一.填空题(本题包括10小题,共30分。)
1.
![]()
周长=9+9+12=30.
2. ![]()
7. 解:
∵ BD=CD
∴ ∠DBC=∠C=40°
∴ ∠BDA=∠DBC+ ∠C=80°
AB=BD
∴ ∠A=∠BDA=80°
∴ ∠ABD=180°-80°-80°=20°
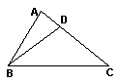
8. 等腰三角形顶角平分线底边上的中线, 底边上的高互相重合.
9. 证明:
∵ ∠MPN=25°, PA=AB=BC=CD
∴ ∠P=∠ABP, ∠BAC=∠CAB, ∠CDB=∠CBD
∠DCM=∠MPN+∠CDP=25°+∠CDB=25°+(25°+∠ACB)
=50°+∠ACB=50°+∠CAB=50°+(∠MPN+∠PBA)
=100°
10. 解:
∵ ∠ACB=90°,
∴ ∠A+ ∠B=∠ACB=90°
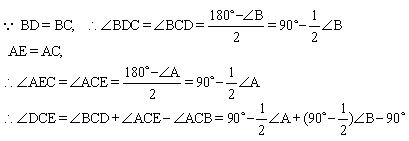
=45°
 .
.
二.单选题(本题包括10小题,共30分。)
3. 注意两种情况
5. 已知: 在△ABC中, AB=AC, CD⊥AB
![]()
证明: 如图: AB=AC, CD⊥AB于D,α=90°-∠B, AB=AC
∴ ∠B=∠ACB
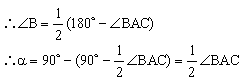
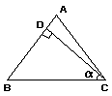
7. 说明:
∵ AB=AC
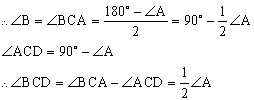
∴∠A=2∠BCD

9. 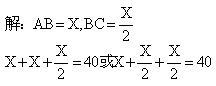
∴ X=16 或 X=20
当 X=20时, BC=10, AC=10
不能构成三角形
∴ AB=16
10. 解: ∠1=∠C+∠2
∵ AB=AC=BD
∴ ∠B=∠C
∴ ∠1=∠B+∠2
∴ ∠1=∠BAD
又 ∠B+∠BAD+∠1=180°
∴ ∠B+2∠1=180°
∠B=∠C, ∠C=∠1-∠2
(∠1-∠2)+2∠1=180°
∴ 3∠1-∠2=180°