初二（上）数学练习卷（十二）

　　　　　  初二（上）数学练习卷（十二）　　　　

班级：____________姓名：_____________学号：____________得分：（2’清洁分）

一、  填空题：（2’×23=46’）

1．的平方根是________________；的整数部分是________________.

2．计算：=________________；=________________.

3．已知：，则x = ____________.

4．已知y – 3与x成正比例，且x = 4时，y = – 1，那么y与x之间的函数解析式是____________.

5．一个弹簧原有长度10厘米，挂上物体后，每增加1千克，弹簧伸长0.4厘米，弹簧长度不得超过20厘米。写出弹簧长度y（厘米）与物体重量x（千克）之间的函数解析式____________________，自变量的取值范围是_____________.

6．函数的定义域为_____________；已知，则y = _____________.

7．函数和的图象的交点坐标是__________________________.

8．解方程：的解为____________________.

9．已知直角三角形斜边上的中线和高分别为5和4，则这个直角三角形的面积为__________.

10．若等腰三角形一腰上的高等于腰长的一半，则此三角形的底角是__________________.

11．已知三角形两边长为2和3，那么第三边上的中线的长的范围是____________________.

12．若正比例函数y = kx（k≠0）与反比例函数在各自的象限内均有y随x的增大而增大，则两个函数_____________（“有”或“没有” ）交点。

13．已知点和是的图象上的点，

若，则比较大小.

14．已知A（2，6），B（– 2，3），AC∥x轴，BC∥y轴且交于点C，

则过点C的正比例函数解析式为________________.

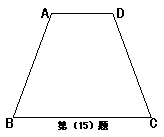
15．如图，在等腰梯形ABCD中，AD∥BC，且AD = 4，BC = 9，又∠C = 90°–∠B，则AB = _____________。

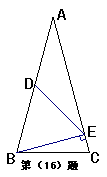
16．如图，在△ABC中，AB = AC，BE⊥AC，D是AB的中点，且DE = BE，则∠C的度数是____________。

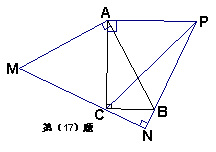
17．在△ABC中∠ACB = 90°，AM⊥AB，且AM = AB，BN⊥MC交MC的延长线于N，AP⊥AC交NB所在的直线于P，那么∠ACP的度数为________________。

18、在△ABC中，AC = 6，AB= 12，∠BAC的平分线与BC的中垂线相交于点O，OM⊥AB（或其延长线）于M，ON⊥AC（或其延长线）于N，那么AM的长为_____________。

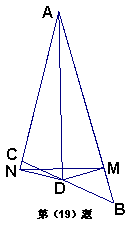
19、AD为△ABC中∠BAC的平分线，DM⊥AB于M，DN⊥AC（或其延长线）于N，又∠DMN的度数为15°，则∠BAC的度数为______________°。

20．在x轴上的动点M到点P（5，5）、Q（2，1）的距离分别为

　　 MP和MQ，那么当MP + MQ取最小值时，点M的坐标是______________.

二、  选择题：（3’×5=15’）

1．  若不等式mx + n < 0的解集是x > 4，点（1，n）在双曲线上，

那么函数的图象不经过　　　　　　　　  （　　　　）

（A）第一象限；　 （B）第二象限；　 （C）第三象限；　 （D）第四象限.

2．已知abc≠0，且，那么直线y = px + p一定经过（　　 ）

（A）第一、二象限；（B）第二、三象限；（C）第三、四象限；（D）第一、四象限.

3．给定直线3x + 2y = 6关于直线y = x对称的直线方程为　　　　　　　  （　　　 ）

（A） 3x – 2y = 6； （B） 2y – 3x =6； （C） 3x + 2y = – 6； （D） 2x + 3y = 6.

4．已知点A（– 2，y₁），B（– 1，y₂），C（3，y₃）都在反比例函数的图象上，则有　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　　　  ）　

（A）y₁ < y₂ < y₃；　（B）y₃ < y₂ < y₁；　（C）y₃ < y₁ < y₂；　（D）y₂ < y₁ < y₃.

5．设b > a，将一次函数y = bx + a与y = ax + b的图象在同一平面直角坐标系内，则有一组a、b的取值，使下列图中的一个为正确的是　　　　　　　　　　  （　　　　）

三、简答题：（6’+6’+8’）

1．已知一次函数y = kx + b，当 – 3≤x≤1时，对应的y的值为1≤y≤9，

　 求kb的值.

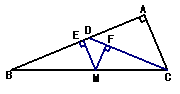
2．如图，△ABC为直角三角形，∠A = 90°，BD = CD，M为BC边上任一点，ME⊥BD于E，MF⊥DC于F

　 求证：ME + MF = AC

3．在y轴上有一点A（0，6），在x轴上有两点B（6，0），C（5，0）

（1）求过AB两点的一次函数解析式及过AC两点的的一次函数解析式。

（2）有一正比例函数y = kx（k > 0）与直线AB交于点E，与直线AC交于点F，若△AEF的面积是四边形EFCB面积的一半，求正比例函数解析式及点E与F的坐标。

四、解答题：

1．有一个附有进、出水管的容器，每单位时间内进、

出的水量都是一定的。设从某时刻开始的5分钟

内只进水不出水，在随后的12分钟内既进水又出水，

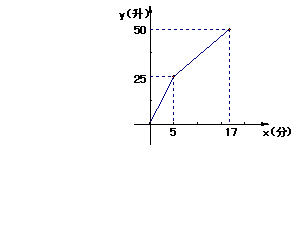
得到时间x（分）与水量y（升）之间的关系如右图所示。

（1）　　　 每分钟进水和出水各多少？（3’）

（2）　　　 5≤x≤17时，写出y关于x的函数解析式。（3’）

（3）　　　 若17分钟后只放水，不进水，

求此时y关于x的函数解析式。（3’）

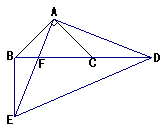2．在Rt△ABC中，AB = AC，D为BC延长线上的一点，连AD，AF⊥AD交BC于F，延长AF到E，使AE = AD，连BE、ED

（1）求证：△BED为直角三角形；（4’）

（2）当点C为DF中点时，分别延长EB、DA相交于点M，

试判断△AMB是什么三角形，并证明你的结论。（4’）