初二年级半期考试数学试卷
一、 择题题（每题4分，共40分）
1、下列函数中，是一次函数的是（ ）
A、y＝-2x2 B、y＝
C、y＝-x+3
D、y＝2x
2、在函数y=x0+
中，自变量x的取值范围是（ ）
A、x≥0 B、 x＞0 C、 x=0 D、x≠0
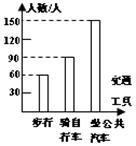
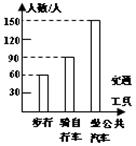
3、如右图所示，下列说法正确的是（ ）
A、步行人最少且为90人;
B、步行人数为50人;
C、坐公共汽车的人数占总数的50%;
D、步行与骑自行车的人数和比坐公共汽车的人数要少.
4、若一次函数y=kx+b的图象经过点（-2,-1）和点（1,2），则这个函数的图象不经过（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
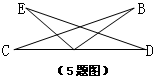
5、不能使两个直角三角形全等的条件是（ ）
A、一条直角边及其对角对应相等 B、两条直角边对应相等
C、斜边和一锐角对应相等 D、两个锐角对应相等
6、如下图所示，已知AC⊥BC，AD平分∠BAC，DE⊥AB，那么下列等式不成立的是（ ）
A、∠ADE=∠ADC B、∠BAC=∠BDE C、DC=DE D、∠ADE=∠BDE
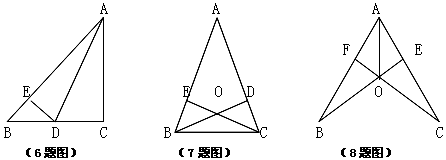
7、如上中图，已知AB=AC，要使△ABD≌△ACE，只需补充条件（ ）
A、∠BOE=∠COD B、∠DOE=∠BOC C、BO=CO D、BO⊥CO
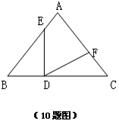
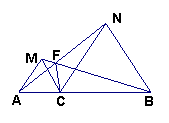
8、如上右图，AD平分∠BAC，AB=AC，连结BD、CD并延长交AC、AB于点E、F，则图中有（ ）对全等三角形。
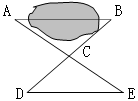A、２ B、３ C、３ D、４
9、如7题图，已知AB=AC，AE=AD，则①△ABD≌△ACE，②△BOE≌△COD，③点O在∠BAC的平分线上，（ ）
A、都正确; B、都不正确; C、只有一个正确; D、只有一个不正确
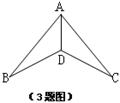
10、如图，有一池塘，要测量池塘两端A、B的距离，可先在平地上取
一个可以直接到达A和B的点C，连结AC并延长至E，使CE=AC，连结BC并延长至D，使CD=BC，连结DE，根据△ABC≌△EDC可知，量出DE的长，就是A、B的距离，这里△ABC≌△EDC的依据是（ A ）
A.SAS B.ASA C.AAS D.SSS
二、填空题（每题4分，共48分）
1、已知：函数
,自变量x的取值范围是_________.
2、已知：函数
为正比例函数，则k＝
3、如图，已知：CD=BD，要得到△ADC≌△ADB，则还需要补充的条件是 _______ .
4、把直线
向上平移2个单位，得到的直线解析式为__________.
5、如图，若△ABC≌△ADE，∠EAC=35°,则∠BAE= ________
|
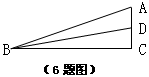
6、如图，在Rt△ABC中，∠C=90°，BD平分∠ABC，若CD=2，AB=8，则△ABD的面积是
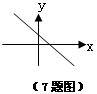
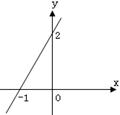
7、已知:一次函数y＝（k－1）x＋k的图象如图所示,则k的取值范围_______
8、若一次函数y＝－x＋m²与y＝4x－1的图象交于x轴，则m的值为 ___
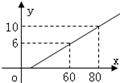
9、某地长途汽车客运公司规定旅客可以随身携带一定重量的行李，如果 超过规定，则需购买行李票，行李票费用y（元）是行李重量x（千克）的一次函数，图象如图，则旅客最多可以免费携带 千克行李。
10、已知:如图，△ABC中，∠B=∠C=50°,BD=CF,BE=CD,则∠EDF= 度.
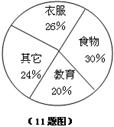
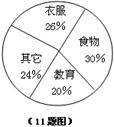
11、小明家上月的开支情况如图所示，其中教育上的支出是150元，则食物上的支出是 元。
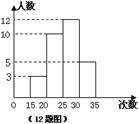
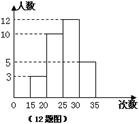
12、为了了解某校八年级学生的体能情况，随机抽查了其中30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图所示的频数分布直方图，请根据图示计算，仰卧起坐次数在25—30次的频率是 。
三、解答题
1、 如图，平面直角坐标系中画出了函数y=kx+b的图象，
⑴ 根据图象，求k、b的值；（4分）
⑵ 在图中画出函数y=–2x+2的图象；（4分）
⑶ 求x的取值范围，使函数y=kx+b的函数值大于函数y=–2x+2的函数值。（5分）
2、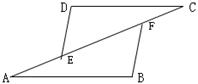 
如图，AB∥CD，AE=CF，AB=CD。
求证：DE=BF. （8分）
3、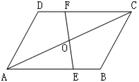 
如图，AB=CD，AD=BC，EF经过AC的中点O，分别交AB、CD于E、F。 求证：OE=OF.（10分）
4、 
如图:矩形ABCD的长为2,宽为1,现有一动点P（不与A
重合）由A→D→C→B运动，使△ABP的面积为y,P点运
动的路程为x，求y关于x的函数解析式及图象。（8分）
5、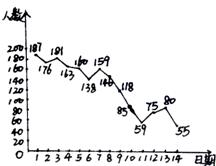 
2003年我国内地发生了“非典型肺炎”疫情，在党和政府的正确领导下，目前疫情已得到有效控制，下图是该年5月1日至5月14日的内地新增确诊病例数据走势图（数据来源：卫生部每日疫情通报），从图中可知道：
⑴5月6日新增确诊病例人数为 _____ 人;（3分）
⑵在5月9日至5月11日的三天中，共新增确诊病例人数为 ______人；（3分）
⑶从右图可看出，5月上半月新增确诊病例总体呈 趋势。（3分）
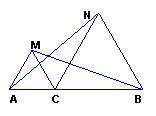
6、⑴已知：如图1，点C为线段AB上一点，△ACM，△CBN是等边三角形，
求证：AN=BM，这时可以证明 __________________，得到AN=BM （4分）
⑵如果去掉“点C为线段AB上一点”的条件,而是让△CBN绕点C旋转成图2的情形,还有“AN=BM”的结论吗?如果有,请给予证明. (5分)
⑶如图3,仍保留原题的所有条件,并设AN、BM交于点F,连接CF,请用刻度尺度量BF、CF、NF的大小,不难发现：BF=CF+NF,为什么?请给予证明. (5分)
试卷答案
(2005.11)
一、 择题题（每题4分，共40分）
1、下列函数中，是一次函数的是（ C ）
A、y＝-2x2 B、y＝ C、y＝-x+3
D、y＝2x
2、在函数y=x0+中，自变量x的取值范围是（ B
）
A、x≥0 B、 x＞0 C、 x=0 D、x≠0
3、如右图所示，下列说法正确的是（ C ）
A、步行人最少且为90人
B、步行人数为50人
C、坐公共汽车的人数占总数的50%
D、步行与骑自行车的人数和比坐公共汽车的人数要少
4、若一次函数y=kx+b的图象经过点（-2,-1）和点（1,2），则这个函数的图象不经过（ D ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
5、不能使两个直角三角形全等的条件是（ D ）
A、一条直角边及其对角对应相等 B、两条直角边对应相等
C、斜边和一锐角对应相等 D、两个锐角对应相等
6、如下图所示，已知AC⊥BC，AD平分∠BAC，DE⊥AB，那么下列等式不成立的是（ D ）
A、∠ADE=∠ADC B、∠BAC=∠BDE C、DC=DE D、∠ADE=∠BDE
7、如上中图，已知AB=AC，要使△ABD≌△ACE，只需补充条件（ C ）
A、∠BOE=∠COD B、∠DOE=∠BOC C、BO=CO D、BO⊥CO
8、如上右图，AD平分∠BAC，AB=AC，连结BD、CD并延长交AC、AB于点E、F，则图中有（ D ）对全等三角形。
A、２ B、３ C、３ D、４
9、如7题图，已知AB=AC，AE=AD，则①△ABD≌△ACE，②△BOE≌△COD，③点O在∠BAC的平分线上，（A）
A、都正确; B、都不正确; C、只有一个正确; D、只有一个不正确
10、如图，有一池塘，要测量池塘两端A、B的距离，可先在平地上取
一个可以直接到达A和B的点C，连结AC并延长至E，使CE=AC，连结BC并延长至D，使CD=BC，连结DE，根据△ABC≌△EDC可知，量出DE的长，就是A、B的距离，这里△ABC≌△EDC的依据是（ A ）
A.SAS B.ASA C.AAS D.SSS
二、填空题（每题4分，共48分）
1、已知：函数,自变量x的取值范围是 x≥1且x≠2
2、已知：函数为正比例函数，则k＝
1
3、如图，已知：CD=BD，要得到△ADC≌△ADB，则还需要补充的条件是 AB＝AC（只要对就行）
4、把直线向上平移2个单位，得到的直线解析式为 
5、如图，若△ABC≌△ADE，∠EAC=35°,则∠BAE= 110°
|
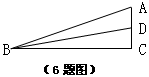
6、如图，在Rt△ABC中，∠C=90°，BD平分∠ABC，若CD=2，AB=8，则△ABD的面积是 8
7、已知:一次函数y＝（k－1）x＋k的图象如图所示,则k的取值范围 0＜k＜1
8、若一次函数y＝－x＋m²与y＝4x－1的图象交于x轴，则m的值为 ± 0.5
9、某地长途汽车客运公司规定旅客可以随身携带一定重量的行李，如果 超过规定，则需购买行李票，行李票费用y（元）是行李重量x（千克）的一次函数，图象如图，则旅客最多可以免费携带 30 千克行李。
10、已知:如图，△ABC中，∠B=∠C=50°,BD=CF,BE=CD,则∠EDF= 50 度.
11、小明家上月的开支情况如图所示，其中教育上的支出是150元，则食物上的支出是 225 元。
12、为了了解某校八年级学生的体能情况，随机抽查了其中30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图所示的频数分布直方图，请根据图示计算，仰卧起坐次数在25—30次的频率是 0.4 。
三、解答题
6、 
如图，平面直角坐标系中画出了函数y=kx+b的图象，
⑴ 根据图象，求k、b的值；（4分）
⑵ 在图中画出函数y=–2x+2的图象；（4分）
|
解：（1）∵函数过点（－1,0）和（0,2），代入y＝kx＋b得
得
∴y＝2x＋2
（2）见图
（3）要使y＝2x＋2的函数值大于函数y＝－2x＋2的函数值，就是前一个函数的图象在后一个函数的上方，
∴x＞0
7、 如图，AB∥CD，AE=CF，AB=CD。 求证：DE=BF （8分）
证明：∵AB∥CD
∴∠A＝∠C
∵AE＝CF
∴AF＝CE
∵AB＝CD
∴△ABF≌△CDE
∴DE＝BF
8、 如图，AB=CD，AD=BC，EF经过AC的中点O，分别交AB、CD于E、F。 求证：OE=OF （10分）
证明：∵AB＝CD，AD＝CB，AC＝CA
∴△ABC≌△CDA
∴∠OAE＝∠OCF
∵∠AOE＝∠COF，O为AC中点
∴AO＝CO
∴△AOE≌△COF
∴OE＝OF
如图:矩形ABCD的长为2,宽为1,现有一动点P（不与A
重合）由A→D→C→B运动，使△ABP的面积为y,P点运
动的路程为x，求y关于x的函数解析式及图象。（8分）
解：
函数为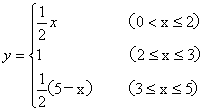
图象略
9、 2003年我国内地发生了“非典型肺炎”疫情，在党和政府的正确领导下，目前疫情已得到有效控制，下图是该年5月1日至5月14日的内地新增确诊病例数据走势图（数据来源：卫生部每日疫情通报），从图中可知道：
⑴5月6日新增确诊病例人数为 138 人;（3分）
⑵在5月9日至5月11日的三天中，共新增确诊病例人数为
262 人；（3分）
⑶从右图可看出，5月上半月新增确诊病例总体呈 下降 趋势。（3分）
6、⑴已知：如图1，点C为线段AB上一点，△ACM，△CBN是等边三角形，
求证：AN=BM，这时可以证明 △ACM ≌ △MCB ，得到AN=BM （4分）
⑵如果去掉“点C为线段AB上一点”的条件,而是让△CBN绕点C旋转成图2的情形,还有“AN=BM”的结论吗?如果有,请给予证明. (5分)
⑶如图3,仍保留原题的所有条件,并设AN、BM交于点F,连接CF,请用刻度尺度量BF、CF、NF的大小,不难发现：BF=CF+NF,为什么?请给予证明. (5分)
|
（2）成立。方法同（1）略
（3）在BF上取一点E，使得BE＝NF，
由（1）知∠CNF＝∠CBE，由CB＝CN得
△ CBE≌△CNF，∴CF＝CE，∠BCE＝∠NCF，
∴∠ECF＝60°即△CEF为等边三角形
∴CF＝EF，∴BF＝CF＋NF。