八年级数学
（上）学期段考试题
一、选择题（每题3分，共24分）
1、在某扇形统计图中，其中一部分的扇形面积所对应的圆心角是120o,那么它所表示的部分占总体的（ ）
（A） 
（B） 
（C） 
（D） 
2、某企业销售主管调查了一个季度本单位产品销售变化情况，并绘制成统计图，你认为较为适用的统计图是（ ）
（A）折线统计图 （B）扇形统计图（C）条形统计图（D）直方统计图
3、某次数学测验，其中一道解答题（满分5分）的得分情况如下表：
| 得分/分 | 0 | 1 | 2 | 3 | 4 | 5 |
| 得该分的人数所占的百分率/% | 20 | 15 | 20 | X | 20 | 5 |
则x等于（ ）
（A）30（B）25（C）40（D）20
4、在下列函数中， y是x的正比例函数的是（ ）
（A） y = 3x－1（B）y = 3x2（C）y = －x（D）y = 
5、直线y=kx＋b与y轴交于点（0，－3）且k＜0,则x＜0时，y的取值范围是（ ）
（A）y＜0（B）y>0（C）y＜－3（D）y>－3
6、一次函数y=kx＋2经过点（1，1），那么这个一次函数（ ）
（A）图象经过原点（B）图象不在第二象限（C）y随x的增大而增大（D）y随x的增大而减少
7、直线y=2x＋b经过点（3，1），则这直线的解析式是（ ）
（A） y=2x＋5（B）y=2x－5（C）y=－2x＋5（D）y=－2x－5
8、根据如图（1-8）的程序计算函数值，若输入的x值为1.5，则输出的结果为（ ）
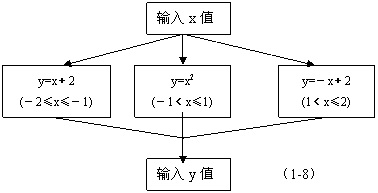
（A） 3.5 （B） 2.25 （C） 0.5 （D） 1.5
二、 填空题（每题3分，共36分）
1、 直线y=－2x—4与x轴的交点坐标为
2、 函数y= x—2中自变量x的取值范围是
3、 已知点A在第四象限，且A到x 轴的距离为5，到y轴的距离为3，则点A的坐标为
4、 如果y=（m2＋1）x是正比例函数，则m的取值范围是
5、 若直线y=3x－1与y=x＋k的交点在第二象限，则k的取值范围是
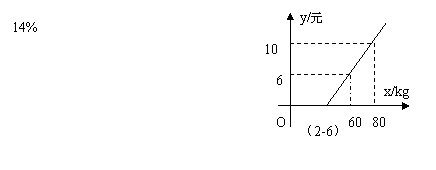
6、 长途客运汽车公司规定乘客可随身携带一定重量的行李，如果超过规定，则需要购买行李票行李费用y（元）是行李重量x（kg）的一次函数，其图象如图（2-6），则y与x之间的函数关系是 ，自变量x的取值是
7、 请你写出一个图象经过（2，1）函数解析式
8、 已知一次函数y=kx－3,请你补充一个条件： ，使y随x的增大而减小
9、在函数y=－2x－5中，当自变量x满足 时，图象在第三象限
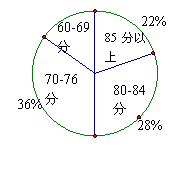
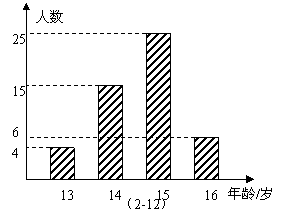10、图（2-10）是某校八年级六班50名学生的依次数学测验成绩的扇形统计图，按图中划分的分数段，这次测验成绩中所占百分比最大的分数段是
；85分以上的共有 人
|
11、对150个数据进行整理得到频数分
布直方图，测得所有长方形的高之和
为33cm，其中最大的小长方形的高
为11cm，则这个最大的长方形所表
示的频数为
12、图3是某班全体学生的年龄的频数分
布直方图，根据图中提供的信息可知该班
学生年龄的平均数是
三、解答题
1、 已知y是x的一次函数，其图象经过点（—2，4），且当x=1时，y=2,求这个一次函数的解析式。（8分）
2、 如图（3-2），正方形ABCD的边长为4，P为DC上一点，设DP=x，求△APD的面
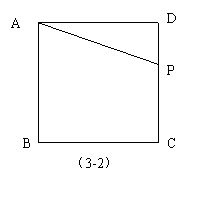积y关于x的函数关系式；并画出这个函数图象. （8分）
3、 （12分）下面是医院对一位病人的体温记录折线图，看图请回答下列问题：
（1） 护士每隔几小时给病人量一次体温？
（2） 这个病人的最高体温是多少摄氏度？
最低体温是多少摄氏度？
（3） 该病人在4月8日12时的体温是多
少摄氏度？
（4） 图中的虚线表示什么？
4、 已知一次函数y=（2m－1）x＋m＋5,求m为何值时：（1）函数值随x的增大而增大；（2）函数值随x的增大而减少。（12分）
5、（8分）一次函数y=kx＋b的自变量x的取值范围是－3≤x≤6，相应的函数值y的取值范围是－5≤y≤－2，求这个函数的解析式。
6、 学校召开运动会，准备从初三年级200名男生中挑选40名同学组成红旗方阵队，为调查男生的身高情况，抽取部分男生的体检表，进行数据整理，得频率分布表如下：
| 分组/cm | 频数 | 频率 |
| 160.5~163.5 | 2 | 0.10 |
| 163.5~166.5 | 3 | a |
| 166.5~169.5 | 5 | 0.25 |
| 169.5~172.5 | 6 | 0.30 |
| 172.5~175.5 | b | 0.20 |
根据表中提供的信息，解答下列问题：（1）本次调查中抽查了多少名学生的体检表？（2）求a，b的值。（3）结合图中信息，为使方阵中学生身高尽可能接近，你认为如何挑选红旗方阵队的同学。（12分）
 |