八年级12月份月考数学试题

八年级12月份月考数学试题

一、选择题（每题3分，共24分）

1、下列图形：①三角形，②线段，③正方形，④直角．其中是轴对称图形的个数是（　）

　　A．4个　　 B．3个　　 C．2个　　 D．1个

　2、等腰三角形的一个内角是50°，则另外两个角的度数分别是（　）

　　  A　65°，65°　　　　　　　　 B　50°，80°

　　  C　65°，65°或50°，80°　　D　50°，50°

3、如果等腰三角形两边长是6cm和3cm，那么它的周长是（　）

　　　A　 9cm　　　B　 12cm　　C　 12cm或15cm　　D　　 15cm

4、等腰三角形是轴对称图形，它的对称轴是

A、过顶点的直线　 B、底边上的高　 C、顶角的平分线　 D、底边的垂直平分线

5、四个图形中，是轴对称图形的有（　 ）

A. 4个　　　B. 3个　 　 C. 2个　 　　 D. 1个

6、在△ABC和△DEF中，①AB=DE, ②BC=EF, ③AC=DF, ④∠A=∠D, ⑤∠B=∠E ,⑥∠C=∠F,不能保证△ABC≌△DEF的一组是　　　　  （　　 ）

（A） ① ② ③　 (B) ① ② ⑤　 (C) ① ③ ⑤　 (D) ② ⑤ ⑥

7、下列说法中，正确的是（　　）

 A  两腰对应相等的两个等腰三角形全等　　  B　两锐角对应相等的两个直角三角形

C 两角及其夹边对应相等的两个三角形全等　 D 面积相等的两个三角形全等

8、点（4，5）关于x=1的对称点的坐标是（　）

A．（-4，5）　　 B．（4，-5）　　 C．（-2，5）　　D．（5，5）

二、填空题（每题3分，共36分）

1、分别写出成轴对称的1个汉字、1个阿拉伯数字和1个英文大写字母______　　　　　 。

2、在电脑中用英文写的英文，其中一句倒排 ：

则正确的英文为____________．

3、一个等腰三角形的底角是顶角的2倍，则该三角形的各个角的度数分别是　　   。

  4、等腰三角形的一腰上的高与底边夹角为12^o，则顶角的度数为____。

　5、关于直线EF对称的两个图形_________（填“一定”或“不一定”）全等．

　6、小丽在镜子里看到对面墙上电子钟示数为 ，则此时实际时刻为_________．

7、已知P₁，P₂关于y轴对称，P₂（-2，3），则P₁的坐标为________．

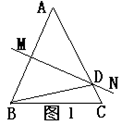
8、如图1，AB=AC，∠A=40^o,AB的垂直平分线MN交AC于点D，则∠DBC=_______。

9、如图2在△ABC中，AB=AC，AB的垂直平分线与AC所在直线相交所得的锐角为40°，则底角∠B=_______．

　

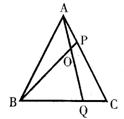
10、如图3,△ABC是等边三角形，在AC、BC边上各取一点P、Q，使AP=CQ，AQ、BP交于点O，则∠QOB=________．

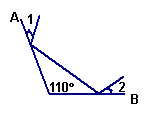
11、如图4，两平面镜A、B之间的夹角为110°,光线经平面镜A反射到平面镜B上，再反射出去，若∠1 =∠2，则∠1=_____ 。

　　　　　 

图2

图3

图4

　　　　

12、等腰三角形一腰的中线把三角形的周长分成24cm和15cm两部分，则这个等腰三角形的底边长是　　　　  。

三、解答题

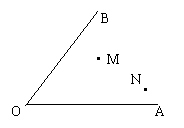1、作图题：如图，求作一点P，使P到AB、AC的距离相等，且使PM=PN。（不要写出画法，但要保留作图痕迹）（7分）

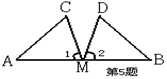
2、已知M是AB的中点，∠1=∠2，∠C=∠D。

 求证： △AMC≌△BMD；（7分）

　

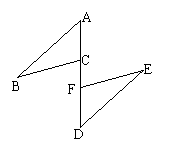3、已知：如图。A、C、F、D在同一直线上，AF=DC，AB=DE，BC=EF，

求证：AB∥DE　 （7分）

4、如图，已知CD平分∠ACB，AE∥DC，交BC的延长线于点E，求证：△ACE是等腰三角形

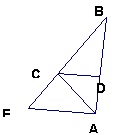（7分）

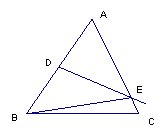5、如图，△ABC中，AB=AC=12,DE垂直平分AB交AC于E，垂足为D，若BC＝7，求△BCE的周长.（7分）

6、已知：如图△ABC中，AB=AC，∠C=30°，AB⊥AD，AD=4cm，

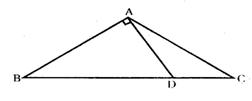求BC的长．（7分）

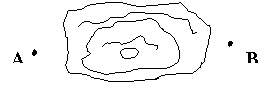7、如图是一座小山的俯视图，在建设桂柳高速公路的过程中，需要打一直线隧道穿过这座小山，要求测量出隧道AB的长度，求你利用所学的三角形全等的知识设计一种测量的方案，并说明理由（8分）

8．如图所示，等边三角形ABC中，AB=2，点P是AB边上的任意一点（点P可以与点A重合

但不与点B重合），过点P作PE⊥BC，垂足为E，过E作EF⊥AC，垂足为F，过F作FQ⊥

AQ，垂足为Q，设BP=x，AQ=y．

（1）写出y与x之间的函数关系式；

（2）当BP的长等于多少时，点P与点Q重合？（10分）