八年级(上)数学期中数学试卷
一.你能填得又快又对吗?(每格3分,共30分)
1.若点(1,3)在正比例函数y=kx的图象上,则此函数的解析式为________.
2.若一次函数y=kx+b交于y轴的负半轴,且y的值随x的增大而减少,则k____0,b______0.(填“>”、“<”或“=”)
3.已知直线y=x-3与y=2x+2的交点为(-5,-8),则方程组![]() 的解是________.
的解是________.
4.如果直线y=-2x+k与两坐标轴所围成的三角形面积是9,则k的值为_____.
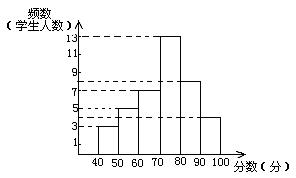
5.某班学生的数学成绩(分数均为正整数)的频数分布直方图如图所示,根据图示信息填空:
(1)该班有学生 人;
(2)如果以大于等于80分为优秀,那么该班的优秀率为 .
6.一个扇形统计图中,某部分占总体的30%,则表示该部分的扇形的圆心角为 度.
7.把64个数据分成8组,第1组到第7组的频数分别是5,6,11,10,8,8,8,那么第8组的频数是 .
8.已知20个数据;68,69,70,66,68,65,64,65,69,62,67,66,65,67,63,65,64,61,65,66 ,在列频率分布表时如果取组距为2,那么应分成 组。
二. 相信你一定能选对!(每小题4分,共40分)
9.下列函数中,y是x的正比例函数的是( )
A.y=2x-1 B.y= ![]() C.y=2x2 D.y=-2x+1
C.y=2x2 D.y=-2x+1
10.下面哪个点在函数y=![]() x+1的图象上( )
x+1的图象上( )
A.(2,1) B.(-2,1) C.(2,0) D.(-2,0)
11.一次函数y=-5x+3的图象经过的象限是( )
A.一、二、三 B.二、三、四
C.一、二、四 D.一、三、四
12.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的解析式为( )
A.y=-x-2 B.y=-x-6 C.y=-x+10 D.y=-x-1
13.李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,如果准时到校.在课堂上,李老师请学生画出他行进的路程y(千米)与行进时间t(小时)的函数图象的示意图,同学们画出的图象如图所示,你认为正确的是( )

14.频率不可能取到的数值是( ).
A.0 B.![]() C.1 D. 1.7
C.1 D. 1.7
15. 能清楚地看出各部分与总体之间的百分比关系的是( ).
A.条形统计图 B.扇形统计图 C.折线统计图 D.以上均可以
16.在频数分布直方图中,每一个小长方形的高等于( )
A.组距 B.组数 C.每个小组的频数 D.每个小组的频率
17.根据下列统计图回答图后问题:
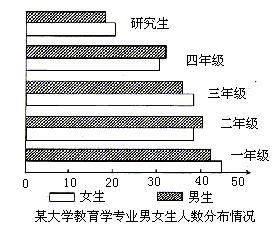
(1)这个专业女生人数最少的年级为:( )
A.一年级 B.二年级 C.四年级 D.研究生
(2)以下判断正确的是:( )
A. 一、二年级总人数比三、四年级总人数少
B. 四年级总人数比二年级总人数多
C.三年级男生比女生少
D. 以上都错
三、认真解答,一定要细心哟!(共80分)
18.(6分)如果y![]() 与x成正比例,且x=3时,y=7。
与x成正比例,且x=3时,y=7。
求y与x之间的函数关系式。
19.(6分)利用图像解不等式:5x-1 >2x+5
20.(8分)柴油机在工作时油箱中的余油量Q(千克)与工作时间t(小时)成一次函数关系,当工作开始时油箱中有油40千克,工作3.5小时后,油箱中余油22.5千克。
(1)写出余油量Q与时间t的函数关系式;(2)画出这个函数的图象。
21.(8分)某电台“市民热线”对上周内接到的热线电话进行了分类统计,得到的统计信息如图所示,其中有关房产城建的电话有30个.请你根据统计图回答以下问题:
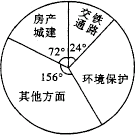
上周“市民热线”共接到电话多少个?上周“市民热线”接到有关环境保护方面的电话多少个?
22.(8分)作出函数y=-2x-5的图象,观察图象回答下列问题:
① x取什么值时,-2x-5=0?
② x取什么值时,-2x-5>0?
③ x取什么值时,-2x-5≤0?
④ x取什么值时,-2x-5<3
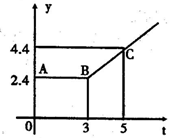
23.(8分)如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.
(1)写出y与t之间的函数关系式.
(2)通话7分钟应付通话费多少元?
24.(8分)如图是某单位职工年龄(取正整数)的频数分布直方图(每组可含最低值,不含最高值),根据图形提供的信息,回答下列问题(直接写出答案):
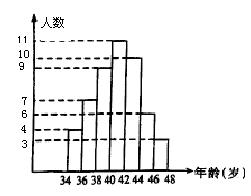
(1)该单位职工共有多少人?
(2)不小于38岁但小于44岁的职工人数占职工总人数的百分比是多少?
(3)如果42岁职工有4人,那么年龄在42岁以上的职工有几人?
25.(8分)下列数据是对我校初一(2)班的同学就"父母回家后,你会主动给他们倒一杯水吗"情况调查结果:主动倒水 27人,偶尔倒水 18人,不倒水 15人.
(1)计算各类人数所占百分比及各个扇形圆心角的度数.
(2)制作扇形统计图,并标上百分比.
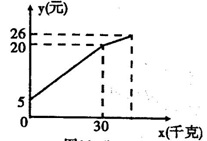
26.(10分)一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
27.(10分)已知雅美服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用A种布料1.1米,B种布料0.4米,可获利50元;做一套N型号的时装需用A种布料0.6米,B种布料0.9米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
①求y(元)与x(套)的函数关系式,并求出自变量的取值范围;
②当M型号的时装为多少套时,能使该厂所获利润最大?最大利润是多?