[科目] 数学
[年级] 初二
[类型] 同步
[关键词] 角平分线
[标题] 角平分线练习
[内容]
角平分线练习
一、选择题
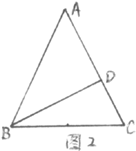
1.已知：如图1，B E，C F是△ABC的角平分线，B E，CF相交于D，若∠A=50°，则∠BDC=（ ）
A. 70° B.120° C.115° D.130°
|
|
2.已知：如图2，△ABC中，AB = AC，BD为∠ABC的平分线，∠BDC = 60°，则∠A =（ ）
A. 10° B. 20°
C. 30° D. 40°
3.三角形中，到三边距离相等的点是（ ）
A.三条高线交点
B.三条中线交点
C.三条角平分线的交点
D.三边的垂直平分线的交点
4.已知P点在∠AOB的平分线上，∠AOB = 60°，OP = 10 cm，那么P点到边OA、OB的距离分别是（ ）
A. 5cm、
cm B. 4cm、5cm
C. 5cm、5cm D. 5cm、10cm
5.下列四个命题的逆命题是假命题的是（ ）
A.直角三角形的两个锐角互余
B.等腰三角形的两个底角相等
C.全等三角形的对应角相等
D.相等的两个角是对顶角
|
|
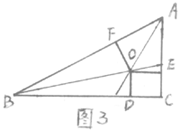
6.已知：如图3，△ABC中，∠C = 90°，点O为△ABC的三条角平分线的交点，OD⊥BC，OE⊥AC，OF⊥AB，点D、E、F分别是垂足，且AB = 10cm，BC = 8cm，CA = 6cm，则点O到三边AB，AC和BC的距离分别等于（ ）cm
A. 2、2、2 B.3、3、3
C. 4、4、4 D. 2、3、5
二、填空题
1.命题：“两直线平行，同旁内角互补”的逆命题是 ，它是 命题。
2.角平分线可以看作是 的点的集合。
3.已知：△ABC中，∠C = 90°，角平分线AD分对边BD：DC = 3：2，且BC = 20cm，则点到AB的距离是 cm。
4.命题“如果a = b，那么 a = b ”的命题是 ，它是 命题。
三、简答题
|
|
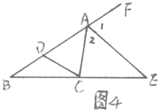
1.已知：如图4，△ABC的外角∠FAC的平分线为AE，∠1=∠2，AD = AC
求证：DC∥AE
|
|
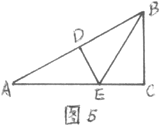
2.已知：如图5，△ABC中，∠C= 90°，点D是斜边AB的中点，AB = 2BC， DE⊥AB交AC于E
求证：BE平分∠ABC
|
|
3.已知线段AB，求线段AB的四等分点。
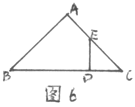
4.已知：如图6，△ABC中，∠A= 90°，AB = AC = BD ED⊥BC
求证：AE = DE =DC
5.已知：线段a和∠a
求作△ABC，使AB = AC = a，∠A= ∠a
【参考答案】
一1. C 2. B 3. C 4. C 5. C 6. A
二1.同旁内角互补，两直线平行， 真
2.到一个角的两边距离相等的所有
3. 8
4.如果 a = b ，那么a = b，假
三1.∵AD = AC，∴∠ADC=∠ACD，△ABC中
∵∠FAC=∠ADC + ∠ACD，
又∠1=∠2=
∠FAC ∴∠ADC=∠FAC=∠1，∴DC∥AE
2.∵D是AB中点 ∴BD=AB，∵AB = 2BC ∴BC=AB ∴BD = BC又∵DE⊥AB∠C=90°，∴∠C=∠BDE=90°，又BE = BE，∴R +△BDE≌Rt△BEC（HL） ∴∠DBE = ∠EBC ∴BE平分∠ABC
3.略
4.连结BE，可证△ABE≌△BDE（HL）∴AE = DE ∵AB = AC ∠A=90° ∴∠C=45°又∵DE⊥BC ∴∠DEC = 45° ∴DE = DC ∴AE = DE = DC
5.略