第二十章 数据分析单元练习题(1)
班级 学号 姓名 得分
一、选择题(每小题3分，共24分)
1．一次数学考试考生约12万名，从中抽取5000名考生的数学成绩进行分析，在这个问题中样本指的是 ( )
A．5000； B．5000名考生的数学成绩；
C．12万考生的数学成绩； D．5000名考生
2．某市社会调查队对城区内一个社区居民的家庭经济状况进行了调查，结果是：该社区共有500户，高收入、中等收入和低收入家庭分别有125户、280户和95户．已知该市有100万家庭，下列表述正确的是 ( )
A．该市高收入家庭约25万户； B．该市中等收入家庭约56万户；
C．该市低收人家庭约19万户；
D．因为城市社区家庭经济状况较好，所以不能据此估计全市所有家庭经济状况。
3．某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%、20％、30％的比例计入学期总评成绩，90分以上为优秀．甲、乙、丙三人的各项成绩如下表(单位：分)，学期总评成绩不是优秀的是 ( )
| 纸笔测试 | 实践能力 | 成长记录 | |
| 甲 | 90 | 83 | 95 |
| 乙 | 88 | 90 | 95 |
| 丙 | 90 | 88 | 90 |
A．甲 B．乙、丙 C．甲、乙 D．甲、丙
4．某“中学生暑期环保小组”的同学，随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量，数据如下(单位：只)：6，5，7，8，7，5，8，lO，5，9．利用上述数据估计小区2000户家庭一周内需要环保方便袋约 ( )
A．2000只 B．14000只 C．21000只 D．98000只
5．下列调查中，适合用普查方法的是 ( )
A．电视机厂要了解一批显像管的使用寿命; B．要了解我市居民的环保意识
C．要了解我市中学生在校时间; D．要了解你校数学教师的年龄状况
6．某班七个合作学习小组人数如下：5，5，6，x，7，7，8．已知这组数据的平均数是6，则这组数据的中位数是 ( )
A．7 B．6 C．5.5 D．5
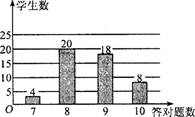
7．数学老师布置10道选择题作为课堂练习，课代表将全班同学的答题情况绘制成条形统计图．根据此图可知，每位同学答对的题数所组成样本的中位数和众数分别为 ( )
A．8，8 B．8，9
C．9，9 D．9，8
8．在一次向“希望工程”捐款的活动中，已知小刚的捐款数比他所在学习小组中13人捐款的平均数多2元，则下列判断中，正确的是
A．小刚在小组中捐款数不可能是最多的；
B．小刚在小组中捐款数可能排在第12位；
C．小刚在小组中捐款数不可能比捐款数排在第7位的同学的少；
D．小刚在小组中捐款数可能是最少的。
二、填空题(每小题4分，共24分)
9．在2005年全国初中数学联赛中，抽查了某县10名同学的成绩如下(单位：分)
78，77，76，74，69，69，68，63，63，63．在这一问题中，样本容量是 ，众数是 ，平均分是 ．
10．2005年5月16日，是世界第十五个助残日，这天某校教师为本区的特殊教育中心捐款的情况如下表：(单位：元)
| 捐款人数 | 32 | 11 | 9 | 21 | 8 | 4 |
| 捐款金额 | 20 | 30 | 40 | 50 | 100 | 200 |
该校教师平均每人捐款约 元(精确到l元)．
11．已知数据a、b、c的平均数为8，那么数据a+l，b+2，c+3的平均数是 ．
12．已知一组数据：－2，－2，3，－2，x，－1，若这组数据的平均数是0.5．则这组数据的中位数是 ．
13．为了解光明中学某班学生每天的睡眠情况，随机抽取该班10名学生在一段时间里每人每天的睡眠时间统计如下(单位：小时)：6，8，8，7，7，9，10，7，6，9，由此估计该班多数学生每天的睡眠时间为
小时．
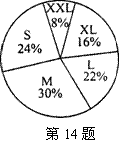
14．右面的扇形图描述了某种品牌服装的S号、M号、L号、XL号、XXL号在一家商场的销售情况．请你为这家商场提出进货建议： ．
三、解答题(52分)
15．(8分)某乡镇企业生产部有技术工人15人，生产部为了合理制定产品的每月生产定额，统计了这15人某月的加工零件个数如下表．
(1)写出15人该月加工零件数的平均数、中位数和众数．
(2)假如生产部负责人把每位工人的月加工零件数定为260件，你认为这个定额是否合理?为什么?
| 每人加工件数 | 540 | 450 | 300 | 240 | 210 | 120 |
| 人 数 | 1 | 1 | 2 | 6 | 3 | 2 |
16．(12分)某同学进行社会调查，随机抽查了某个地区的20个家庭的年收人情况，并绘制了统计图．请你根据统计图给出的信息回答：
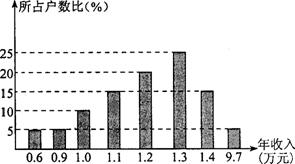
(1)填写完成下表：
| 年收入(万元) | O.6 | O.9 | 1.O | 1.1 | 1.2 | 1.3 | 1.4 | 9.7 |
| 户 数 |
这20个家庭的年平均收入为 万元．
(2)样本中的中位数是 万元，众数是 万元．
(3)在平均数、中位数两数中， 更能反映这个地区家庭的年收入水平．
17．(10分)某水果店有200个菠萝，原计划以2.6元／kg的价格出售，现在为了满足市场需要，水果店决定将所有的菠萝去皮后出售．以下是随机抽取5个菠萝去皮前后相应的质量统计表：(单位：kg)
(1)计算所抽取的5个菠萝去皮前的平均质量和去皮后的平均质量，并估计这200个菠萝去皮前的总质量和去皮后的总质量．
(2)根据(1)的结果，要使去皮后这200个菠萝的销售总额与原计划的销售总额相同，那么去皮后的菠萝的售价应是每千克多少元?
| 去皮前各菠萝的质量 | 1.0 | 1.1 | 1.4 | 1.2 | 1.3 |
| 去皮后各菠萝的质量 | 0.6 | 0.7 | 0.9 | 0.8 | 0.9 |
18．(10分)某校八年级(1)班的一个研究性学习小组的研究课题是某高速公路入口的汽车流量问题．某天上午，他们在该入口处，每隔相等的时间，对3分钟内通过的汽车的数量作一次统计，得到如下数据：www.1230.org 初中数学资源网 jsntrjf
| 记录的次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3分钟内通过的汽车数量 | 49 | 50 | 64 | 58 | 53 | 56 | 55 | 47 |
(1)平均每3分钟通过汽车多少辆?
(2)试估计：这天上午，该人口平均每小时通过多少辆汽车．
19．(12分)某学校对初中毕业班经过初步比较后，决定从初三(1)、(4)、(8)这三个班中推荐一个班为市级先进班集体的候选班．现对这三个班进行综合素质考评，下表是他们五项素质考评的得分表(以分为单位，每项满分为10分)．
| 班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
| 初三(1) | lO | 10 | 6 | lO | 7 |
| 初三(4) | 10 | 8 | 8 | 9 | 8 |
| 初三(8) | 9 | lO | 9 | 6 | 9 |
(1)请问各班五项考评的平均分、中位数和众数中哪个统计量不能反映三个班的考评结果的差异?并从中选择一个能反映差异的统计量将他们的得分进行排序．
(2)根据你对表中五个项目的重要程度的认识，设定一个各项考评内容的占分比例(比例的各项须满足：①均为整数；②总和为10；③不全相同)，按这个比例对各班的得分重新计算，比较出大小关系，并从中推荐一个得分最高的班级作为市级先进班集体的候选班．
第二十章 数据分析单元练习题(1) 答案：
第二十章 数据分析单元练习题(2)
班级 学号 姓名 得分
一、选择题(每小题4分，共20分) f上传
1．某中学人数相等的甲、乙两班学生参加了同一次数学测验，班平均分和方差分别为
82分，
82分，
245分2，
190分2．那么成绩较为整齐的是 ( )
A．甲班 B．乙班 C．两班一样整齐 D．无法确定
2．体育课上，八年级(1)班两个组各10人参加立定跳远，要判断哪一组成绩比较整齐，通常需要知道这两个组立定跳远成绩的 ( )
A．平均数 B．方差 C．众数 D．中位数
3．已知一组数据x1，x2，x3，x4，x5的平均数是2，方差是
，那么另一组数据3 x1－2，3 x2－2，3 x3－2，3 x4－2，3 x5－2的平均数和方差分别是
( )
A．2， B．2，1 C．4，
D．4，3
4．一台机床在十天内生产的产品中，每天出现的次品个数依次为(单位：个)0，2，0，2，3，0，2，3，1，2．那么，这十天中次品个数的 ( )
A．平均数是2 B．众数是3
C．中位数是1.5 D．方差是1.25
5．甲、乙两班举行电脑汉字输入速度比赛，参加学生每分钟输入汉字的个数经统计计算后填人下表：
| 班级 | 人数 | 中位数 | 方差 | 平均字数 |
| 甲 | 55 | 149 | 191 | 135 |
| 乙 | 55 | 151 | 110 | 135 |
某同学根据上表分析得出如下结论：①甲、乙两班学生成绩的平均水平相同；②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀)；③甲班的成绩的波动情况比乙班的成绩的波动大．上述结论正确的是 ( )
A．①②③ B．①② C．①③ D．②③
二、填空题(每小题4分，共24分)
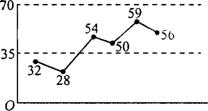6．右图是一组数据的折线统计图，这组数据的极差是 ，平均数是
．
7．数据一2，一1，0，1，2的方差是 ．
|
3，1.2．成绩较为稳定的是 (选填“甲”或“乙”)．
9．若样本数据1，2，3，2的平均数是a，中位数是b，众数是c，则数据a、b、c的方差是 ．
10．一组数据的方差是，
…
,则这组数据共有 个，平均数是 ．
11．设x1，x2，…，xn平均数为
，方差为
．若
，则x1，x2，…，xn应满足的条件是
三、解答题(56分)
12．(10分)某校八年级学生开展踢毽子比赛活动，每班派5名学生参加．按团体总分多少排列名次，在规定时间每人踢100个以上(含100个)为优秀，下表是成绩最好的甲班和乙班5名学生的比赛数据(单位：个)
| 1号 | 2号 | 3号 | 4号 | 5号 | 总分 | |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 86 | 100 | 98 | 119 | 97 | 500 |
经统计发现两班总分相等，此时有学生建议，可通过考查数据中的其他信息作为参考．请你回答下列问题：
(1)计算甲、乙两班的优分率．
(2)求两班比赛数据的中位数。
(3)估计两个比赛数据的方差哪一个小?
(4)根据以上信息，你认为应该把冠军奖状发给哪一个班级?简述理由．
13．(12分)观察与探究．
(1)观察下列各组数据并填空．
A．1 2 3 4 5 
=，
B．11 12 13 14 15 
=，
C．10 20 30 40 50 
=，
D．3 5 7 9 11 
=，
(2)比较A与B、C、D的计算结果，你能发现什么规律?请与你的伙伴交流．
(3)若已知一组数据x1，x2，…，xn平均数为，方差为，那么另一组数据3 x1－2，3 x2－2，…，3xn－2平均数为
，方差为
．
14．(12分)为选派一名学生参加全市实践活动技能竞赛，A、B两位同学在学校实习基地现场进行加工直径为20mm的零件的测试，他俩各加工10个零件的相关数据依次如图所示．
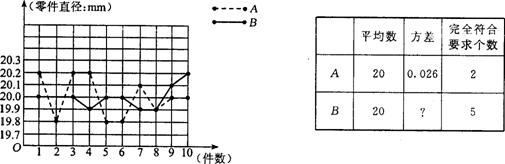
根据测试得到的有关数据，试解答下列问题：
(1)考虑平均数与完全符合要求的个数，你认为 的成绩好些．
(2)计算出B的方差，考虑平均数与方差，说明谁的成绩好些．
(3)考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况，你认为派谁去参赛较合适?说明你的理由．
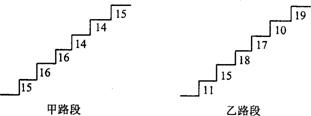
15．(12分)在某旅游景区上山的一条小路上，有一些断断续续的台阶，下图是其中的甲、乙两段台阶的示意图，请你用所学过的有关统计知识(平均数、中位数、极差和方差)回答下列问题：(单位：cm)
(1)两段台阶有哪些相同点和不同点?
(2)哪段台阶走起来更舒服，为什么?
(3)为方便游客行走，需要重新整修上山的小路，对于这两段台阶，在台阶数不变的情况下，请你提出合理的整修建议．
16．(10分)小明和小兵参加某体育项目训练，近期的8次测试成绩(分)如下表：
| 测试 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 |
| 小明 | 10 | 10 | 11 | 10 | 16 | 14 | 16 | 17 |
| 小兵 | 11 | 13 | 13 | 12 | 14 | 13 | 15 | 13 |
(1)根据上表中提供的数据填写下表：
| 平均数 | 众数 | 中位数 | 方差 | |
| 小明 | 10 | 8.25 | ||
| 小兵 | 13 | 13 |
(2)若从中选一人参加市中学生运动会，你认为选谁去合适呢?请说明理由．
第二十章 数据分析单元练习题(2)答案:
第二十章 数据分析单元练习题(3)
班级 学号 姓名 得分
一、选择题
1．数据按从小到大排列为1，2，4，x，6，9，这组数据的中位数为5，那么这组数据的众数是（ ）
（A）4 （B）5 （C）5．5 （D）6
2．在一次区级数学竞赛中，某校8名参赛学生的成绩与全区参赛学生数学平均分80的差分别是5，-2，8，14，7，5，9，-6，则此8名学生数学竞赛的平均成绩是（ ）
（A）80分 （B）84分 （C）85分 （D）88分
3．期中考试后，学习小组长算出该组5位同学数学成绩的平均分为M，如果把M当成另一个同学的分数，与原来的5个分数一起，算出这6个分数的平均值为N，那么M：N为（ ）
（A）
（B）1 （C）
（D）2
4．下列说法错误的是（ ）
（A）一组数据的众数、中位数和平均数不可能是同一个数
（B）一组数据的平均数既不可能大于，也不可能小于这组数据中的所有数据
（C）一组数据的中位数可能与这组数据的任何数据都不相等
（D）众数、中位数和平均数从不同角度描述了一组数据的集中趋势
5．某地区10户家庭的年消费情况如下：2户10万元，1户5万元，6户1．5万元，1户7千元．可估计该地每户年消费金额的一般水平为（ ）
（A）10万元 （B）5万元 （C）1.5万元 （D）3.47万元
6．路旁有一鱼塘，旁边竖着的牌子写明此塘的平均水深为1.5m，小明身高为1.7m，不会游泳，小明跳入鱼塘后的结果是（ ）
（A）一定有危险 （B）一定没有危险
（C）可能有危险也可能没有危险 （D）以上答案都不对
7．将一组数据中每一个数减去50后，所得新的一组数据的平均数是2，则原来那组数据的平均数是（ ）
（A）50 （B）52 （C）48 （D）2
8．一个射手连续射靶22次，其中三次射中10环，7次射中9环，9次射中8环，3次射中7环，则射中环数的中位数和众数分别为（ ）
（A）8，9 （B）8，8 （C）8.5，8 （D）8.5，9
9．某工厂生产一种产品，若10天中每天生产的次品数分别为2，3，1，1，10，2，1，1，0，1，则这个样本的方差是（ ）
（A）0.76 （B）0.504 （C）2.75 （D）0.572
10．一组数据的方差是2，将这组数据都扩大3倍，则所得一组新数据的方差是（ ）．
（A）2 （B）6 （C）32 （D）18
11．在统计中，样本的方差可以近似地反映总体的（ ）
（A）平均状态 （B）波动大小 （C）分布规律 （D）集中趋势
12．若样本x1+1，x2+1，…，xn+1的平均数为10，方差为2，则对于样本x1+2，x2+2，…，xn+2，下列结论正确的是（ ）
（A）平均数为10，方差为2; （B）平均数为11，方差为3;
（C）平均数为11，方差为2; （D）平均数为12，方差为4
13．某工厂对一个生产小组的零件进行抽样检查，在10天中，这个生产小组每天生产的次品数如下（单位：个）：0，2，0，2，3，0，2，3，1，2．在这10天中，该生产小组生产零件所产生的次品数的（ ）
（A）平均数是2; （B）众数是3; （C）中位数是1.5; （D）方差是1.25
14．一组数据：-1，0，4，x，6，15，它们按从小到大排列，且这些数据的中位数为5， 那么这组数据的众数为（ ）
（A）5 （B）6 （C）4 （D）5.5
15．某次体育活动中，统计甲、乙两班学生每分钟跳绳的成绩（单位：次）情况如下表：
| 班级 | 参加人数 | 平均次数 | 中位数 | 方差 |
| 甲班 | 55 | 135 | 149 | 190 |
| 乙班 | 55 | 135 | 151 | 110 |
下面有三个命题：
①甲班学生的平均成绩高于乙班学生的平均成绩．
②甲班学生成绩的波动比乙班学生成绩的波动大．
③甲班学生成绩优秀的人数不多于乙班学生成绩优秀的人数（跳绳次数≥150次为优秀）． 则正确的命题是（ ）
（A）① （B）② （C）③ （D）②和③
二、填空题
16．某青年队队员的年龄情况如下：
| 年龄（岁） | 18 | 19 | 20 | 21 | 22 |
| 人数 | 1 | 4 | 3 | 2 | 2 |
则该队队员的平均年龄是_______．
17．某公司欲招聘工人，对候选人进行三项测试：语言、创新、综合知识，并把测试得分按1：4：3比例确定测试总分，已知某候选人三项得分分别为88，72，50，则这位候选人的招聘得分为________．
18．初中（1）班50人，初二（2）班52人，在期末数学考试中（1）班平均90分，（2）班平均94分，则这两个班的平均成绩约是________．
19．a、b、c三个数的平均数是6，则2a-3，2b-2，2c+5的平均数是________．
20．在演唱比赛中，8位评委给一位歌手的演唱打分如下：9.3，9.5，9.9，9.4，9.3，8.9，9.2，9.6，若去掉一个最高分和一个最低分后的平均分为所得分，则这名歌手最后得分约为________．
21．某公司员工的月工资如下：
| 员工 | 经理 | 副经理 | 职员A | 职员B | 职员C | 职员D | 职员E |
| 月工资（元） | 6000 | 3500 | 1500 | 1500 | 1500 | 1100 | 1100 |
该公司员工月工资的中位数是_______，众数是________．
22．小明家去年的旅游、教育、饮食支出分别为3600元，1200元，7200元，今年这三项支出依次比去年增长10%，20%，30%，则小明家今年的总支出比去年增长的百分数是________．
23．如果一组数据-3，-2，0，1，x，6，9，12的平均数为3，那么这组数据的中位数是___________．
24．数据1，-2，1，0，-1，2的方差是_______．
25．某中学人数相等的甲、乙两班学生参加了同一次数学测验，两班平均分和方差分别为甲=82分，乙=82分，S2甲=245，S2乙=190．那么成绩较为整齐的是________班（填“甲”或“乙”）
三、解答题
26．一家鞋店一段时间里销售一种女鞋20双，其中各种尺码的鞋的销售量如下表：
| 鞋的尺码（cm） | 30 | 28 | 29 | 23 | 21 | 25 |
| 销售量（双） | 5 | 1 | 2 | 3 | 4 | 5 |
（1）求这组数据的平均数、中位数、众数．
（2）你能说出这组数据的中位数、众数的实际意义吗？
27．某研究性学习小组为了了解本校初一学生一天中做家庭作业所用的大致时间（时间以整数记，单位：分钟），对本校的初一学生做了抽样调查，并把调查得到的所有数据（时间）进行整理，分成五个时间段，绘制成统计图（如图所示），请结合统计图中提供的信息，回答下列问题：
（1）这个研究性学习小组所抽取样本的容量是多少？
（2）在被调查的学生中，一天做家庭作业所用的大致时间超过120分钟（不包括120分钟）的人数占被调查学生总人数的百分之几？
（3）这次调查得到的所有数据的中位数落在了五个时间段中的哪一段内？
第二十章 数据分析单元练习题(3)答案:
一、选择题
1．（D） 2．（C） 3．（B） 4．（A） 5．（C） 6．（C） 7．（B） 8．（B） 9．（A） 10．（D） 11．（B） 12．（C） 13．（D） 14．（B） 15．（D）
二、填空题
16．20
17．65.75
18．92
19．12
20．9.4
21．1500元 1500元
22．
=23%
∴小明家今年的总支出比去年增长23%．
23．1 24．
25．乙 www.czsx.com.cn
三、解答题
26．30cm，25cm的鞋各出现5次，所以众数有两个，分别是30cm，25cm，求中位数时应注意，排列数据的顺序及数据出现的次数．本题共有2+4+3+5+1+5=20个数据，第10位数据25cm，第11位数据25cm，所以中位数为（25cm+25cm）÷2=25cm．
（1）这组数据的平均数是24.8cm；中位数是25cm；众数是30cm，25cm．
（2）这组数据中的众数是30cm，25cm，说明销售的女鞋中这两种型号的鞋销售最好，而中位数是25cm，则表示所穿鞋的尺码最多的与销量最好的恰恰是同一型号．
27．解析：（1）3+4+6+8+9=30，故这个研究性学习小组取样本的容量是30．
（2）（9+8+4）÷30=0.7=70%，所以一天做家庭作业所用的时间超过120分钟的学生人数占被调查学生总人数的70%．www.czsx.com.cn
（3）中位数落在了120.5分钟～150.5分钟这个时间段内．