第十八章练习卷（相似三角形的性质及应用）
班级 姓名 座号 评分
一、填空题
1、已知两个相似三角形的相似比为3，则它们的周长比为 ；
2、若△ABC∽△A′B′C′，且
，△ABC的周长为12cm，则△A′B′C′的周长为
；
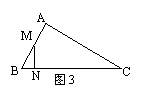
3、如图1，在△ABC中，中线BE、CD相交于点G，则
= ；S△GED：S△GBC= ；
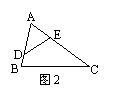
4、如图2，在△ABC中， ∠B=∠AED，AB=5，AD=3，CE=6，则AE=
；
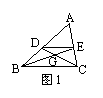
5、如图3，△ABC中，M是AB的中点，N在BC上，BC=2AB，∠BMN=∠C，则△ ∽△ ，相似比为
，
=
；
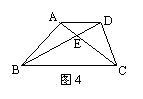
6、如图4，在梯形ABCD中，AD∥BC，S△ADE：S△BCE=4：9，则S△ABD：S△ABC= ；
7、两个相似三角形的周长分别为5cm和16cm，则它们的对应角的平分线的比为 ；
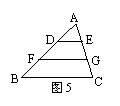
8、如图5，在△ABC中，BC=12cm，点D、F是AB的三等分点，点E、G是AC的三等分点，则DE+FG+BC= ；
9、两个三角形的面积之比为2：3，则它们对应角的比为 ，对应边的高的比为 ；
10、已知有两个三角形相似，一个边长分别为2、3、4，另一个边长分别为x、y、12，则x、y的值分别为 ；
二、选择题
11、下列多边形一定相似的为（ ）
A、两个矩形 B、两个菱形 C、两个正方形 D、两个平行四边形
12、在△ABC中，BC=15cm，CA=45cm，AB=63cm，另一个和它相似的三角形的最短边是5cm，则最长边是（ ）
A、18cm B、21cm C、24cm D、19.5cm
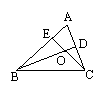
13、如图，在△ABC中，高BD、CE交于点O，下列结论错误的是（ ）
A、CO·CE=CD·CA B、OE·OC=OD·OB
C、AD·AC=AE·AB D、CO·DO=BO·EO
14、已知，在△ABC中，∠ACB=900，CD⊥AB于D，若BC=5，CD=3，则AD的长为（ ）
A、2.25 B、2.5
C、2.75
D、3
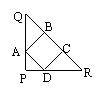
15、如图，正方形ABCD的边BC在等腰直角三角形PQR的底边QR上，
其余两个顶点A、D在PQ、PR上，则PA：PQ等于（ ）
A、1：
B、1：2 C、1：3
D、2：3
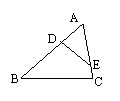16、如图，D、E分别是△ABC的边AB、AC上的点， 
=
=3，
且∠AED=∠B，则△AED与△ABC的面积比是（ ）
A、1：2 B、1：3 C、1：4 D、4：9
三、解答题
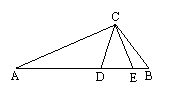
17、如图，已知在△ABC中，CD=CE，∠A=∠ECB，试说明CD2=AD·BE。
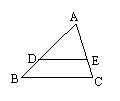18、已知，如图， 在△ABC中，DE∥BC，AD=5，BD=3，求S△ADE：S△ABC的值。
19、已知正方形ABCD，过C的直线分别交AD、AB的延长线于点E、F，且AE=15，AF=10，求正方形ABCD的边长。
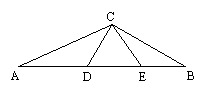20、已知，如图，在等边△CDE中，A、B分别是ED、DE的延长线上的点，且DE2=AD·EB，求∠ACB的度数。
21、已知，如图，在△ABC中，∠C=600，AD⊥BC于D，BE⊥AC于E，试说明△CDE∽△CBA。
 |
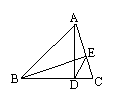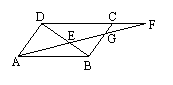
22、已知，如图，F为
ABCD边DC延长线上一点，连结AF，交BC于G，交BD于E，试说明AE2=EG·EF