第十一章《一次函数》复习题
1、(北京市2006)一次函数y=x+3的图象不经过的象限是( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
2、(天津市2006)已知一次函数y=kx+b(k≠0)的图象经过点(0,1),且y随x的增大而增大,请你写出一个符合上诉条件的函数关系式___________________.
 3、(广东省2006)函数
3、(广东省2006)函数![]() 中自变量x的取值范围是 ( )材A.x≠-l B.x
>-1 C.x =- 1 D.x <- 1
中自变量x的取值范围是 ( )材A.x≠-l B.x
>-1 C.x =- 1 D.x <- 1
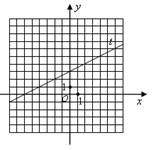
4、(济南市2006)如图,直线![]() 是函数
是函数![]() 的图象.若点
的图象.若点![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 点的坐标可能是( )A
点的坐标可能是( )A![]() B
B![]() C
C![]() D
D![]()
 5、(青岛市2006)点P1(x1,y1),点P2(x2,y2)是一次函数y =-4x + 3 图象上的两个点,且
x1<x2,则y1与y2的大小关系是( ).
5、(青岛市2006)点P1(x1,y1),点P2(x2,y2)是一次函数y =-4x + 3 图象上的两个点,且
x1<x2,则y1与y2的大小关系是( ).
A.y1>y2 B.y1>y2 >0 C.y1<y2 D.y1=y2
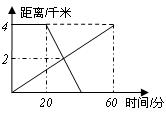
6、(武汉课改2006)已知A、B两地相距4千米。上午8:00,甲从A地出发步行到B的,8:20乙从B地出发骑自行车到A地,甲乙两人离A地的距离(千米)与甲所用的时间(分)之间的关系如图所示。由图中的信息可知,乙到达A地的时间为
A、8:30 B、8:35 C、8:40 D、8:45
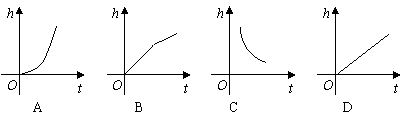
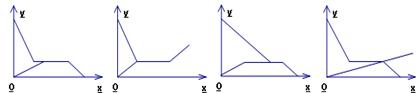
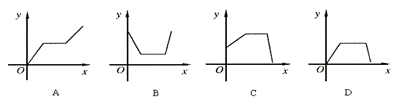 7、(北京海淀2006)打开某洗衣机开关,在洗涤衣服时(洗衣机内无水),洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间满足某种函数关系,其函数图象大致为( )
7、(北京海淀2006)打开某洗衣机开关,在洗涤衣服时(洗衣机内无水),洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间满足某种函数关系,其函数图象大致为( )
8、(山东枣庄市2006)小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是( )
( A ) 37.2分钟 (B) 48分钟 (C ) 30分钟 ( D )33分钟
9、(长沙市2006)某游泳池分为深水区和浅水区,每次消毒后要重新将水注满泳池,假定进水管的水速是均匀的,那么泳池内水的高度![]() 随时间
随时间![]() 变化的图象是( )
变化的图象是( )
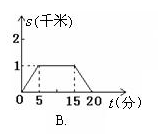
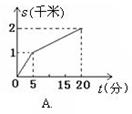
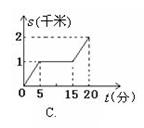
10、(泉州市2006)小明所在学校离家距离为2千米,某天他放学后骑自行车回家,行驶了5分钟后,因故停留10分钟,继续骑了5分钟到家.下面哪一个图象能大致描述他回家过程中离家的距离![]() (千米)与所用时间
(千米)与所用时间![]() (分)之间的关系( ).
(分)之间的关系( ).
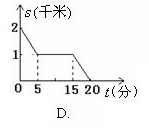
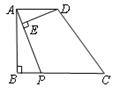 11、(北京市2006)如右图,在梯形ABCD中,AD∥BC,∠B=90°,AD=1,AB=
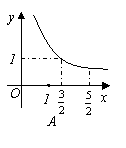
11、(北京市2006)如右图,在梯形ABCD中,AD∥BC,∠B=90°,AD=1,AB=![]() ,BC=2,P是BC边上的一个动点(点P与点B不重合),DE⊥AP于点E。设AP=x,DE=y。在下列图象中,能正确反映y与x的函数关系的是( )
,BC=2,P是BC边上的一个动点(点P与点B不重合),DE⊥AP于点E。设AP=x,DE=y。在下列图象中,能正确反映y与x的函数关系的是( )
 | |||||
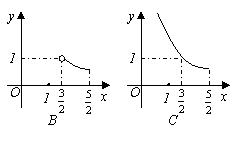 | |||||
 | |||||
12、(常州市2006)已知:如图1,点G是BC的中点,点H在AF上,动点P以每秒2![]() 的速度沿图1的边线运动,运动路径为:
的速度沿图1的边线运动,运动路径为:![]() ,相应的△ABP的面积
,相应的△ABP的面积![]() 关于运动时间
关于运动时间![]() 的函数图像如图2,若
的函数图像如图2,若![]() ,则下列四个结论中正确的个数有( ) ①图1中的BC长是8
,则下列四个结论中正确的个数有( ) ①图1中的BC长是8![]() ,②图2中的M点表示第4秒时
,②图2中的M点表示第4秒时![]() 的值为24
的值为24![]() ,③图1中的CD长是4
,③图1中的CD长是4![]() , ④图2中的N点表示第12秒时
, ④图2中的N点表示第12秒时![]() 的值为18
的值为18![]() .A.1个 B.2个 C.3个 D.4个
.A.1个 B.2个 C.3个 D.4个
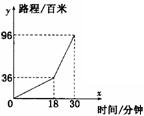
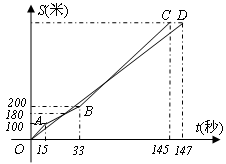 13、(黄冈2006)如图,在光明中学学生耐力测试比赛中,甲、乙两学生测试的路程S(米)与时间t(秒)之间的函数关系图像分别为折线OABC和线段OD,下列说法正确的是( )
13、(黄冈2006)如图,在光明中学学生耐力测试比赛中,甲、乙两学生测试的路程S(米)与时间t(秒)之间的函数关系图像分别为折线OABC和线段OD,下列说法正确的是( )
A、乙比甲先到达终点
B、乙测试的速度随时间增加而增大
C、比赛进行到29.4秒时,两人出发后第一次相遇
D、比赛全程甲的测试速度始终比乙的测试速度快
 14、(贵阳市2006)小明根据邻居家的故事写了一首小诗:“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还。”如果用纵轴
14、(贵阳市2006)小明根据邻居家的故事写了一首小诗:“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还。”如果用纵轴![]() 表示父亲与儿子行进中离家的距离,用横轴
表示父亲与儿子行进中离家的距离,用横轴![]() 表示父亲离家的时间,那么下面的图象与上述诗的含义大致吻合的是( )
表示父亲离家的时间,那么下面的图象与上述诗的含义大致吻合的是( )
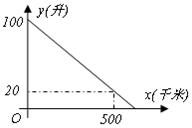 16、(宜昌市2006)某汽车生产厂对其生产的A型汽车进行耗油量实验,实验中汽车视为匀速行驶。已知油箱中的余油量y(升)与行驶时间t(小时)的关系如下表,与行驶路程x(千米)的关系如下图。请你根据这些信息求A型车在实验中的速度。
16、(宜昌市2006)某汽车生产厂对其生产的A型汽车进行耗油量实验,实验中汽车视为匀速行驶。已知油箱中的余油量y(升)与行驶时间t(小时)的关系如下表,与行驶路程x(千米)的关系如下图。请你根据这些信息求A型车在实验中的速度。
| 行驶时间t(小时) | 0 | 1 | 2 | 3 |
| 油箱余油量y(升) | 100 | 84 | 68 | 52 |
| 图号 | 顶点数x | 棱数y | 面数z |
| (a) | 8 | 12 | 6 |
| (b) | |||
| (c) | |||
| (d) | |||
| (e) |
17、(烟台市2006)下列图形中,图(a)是正方体木块,把它切去一块,得到如图(b)(c)(d)(e)的木块.(1)我们知道,图(a)的正方体木块有8个顶点、12条棱、6个面,请你将图(b)、(c)、(d)、(e)中木块的顶点数、棱数、面数填入下表:
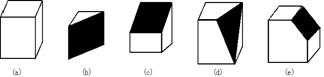 (2)上表,各种木块的顶点数、棱数、面数之间的数量关系可以归纳出一定的规律,请你试写出顶点数x、棱数y、面数z之间的数量关系式.
(2)上表,各种木块的顶点数、棱数、面数之间的数量关系可以归纳出一定的规律,请你试写出顶点数x、棱数y、面数z之间的数量关系式.
18、(温州市2006)矩形的周长是16cm设一边长为xcm,另一边长为ycm.
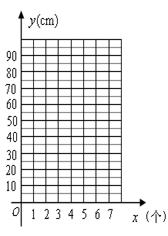
(1)求y关于x的函数关系式,并写出自变量x的取值范围;(2)作出函数图象;
(3)若P(x,y)点是该图象上的一动点,点A的坐标为(6,0),设⊿OPA的面积为S,用含x的解析式表示S
 19、(济南市2006)元旦联欢会前某班布置教室同学们利用彩纸条粘成一环套一环的彩纸链,小颖测量了部分彩纸链的长度,她得到的数据如下表:
19、(济南市2006)元旦联欢会前某班布置教室同学们利用彩纸条粘成一环套一环的彩纸链,小颖测量了部分彩纸链的长度,她得到的数据如下表:
| 纸环数 | 1 | 2 | 3 | 4 | …… |
| 彩纸链长度 | 19 | 36 | 53 | 70 | …… |
(1)把上表中![]() 的各组对应值作为点的坐标,在如图的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在如图的平面直角坐标系中描出相应的点,猜想![]() 与
与![]() 的函数关系,并求出函数关系式;
的函数关系,并求出函数关系式;
(2)教室天花板对角线长10m,现需沿天花板对角线各拉一根彩纸链,则每根彩纸链至少要用多少个纸环?
20、(常州市2006)春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:




某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
21、(武汉市2006)某公司以每吨200元的价格购进某种矿石原料300吨,用于生产甲、乙两种产品。生产1吨甲产品或1吨乙产品所需该矿石和煤原料的吨数如下表:
|
资源 | 甲 | 乙 |
| 矿石(t) | 10 | 4 |
| 煤(t) | 4 | 8 |
煤的价格为400元/吨。生产1吨甲产品除原料费用外,还需其它费用400元,甲产品每吨售价4600元;生产1吨乙产品除原料费用外,还需其它费用500元,乙产品每吨售价5500元。现将该矿石原料全部用完。设生产甲产品x吨,乙产品m吨,公司获得的总利润为y元。(1)写出m与x之间的关系式;(2)写出y与x之间的函数表达式(不要求写出自变量的范围);(3)若用煤不超过200吨,生产甲产品多少吨时,公司获得的总利润最大?最大利润是多少?
22、(青岛市2006)在2006年青岛崂山北宅樱桃节前夕,某果品批发公司为指导今年的樱桃销售,对往年的市场销售情况进行了调查统计,得到如下数据:
| 销售价 x(元/千克) | … | 25 | 24 | 23 | 22 | … |
| 销售量 y(千克) | … | 2000 | 2500 | 3000 | 3500 | … |
 (1)在如图的直角坐标系内,作出各组有序数对(x,y)所对应的点.连接各点并观察所得的图形,判断y与x之间的函数关系,并求出y与x之间的函数关系式;(2)若樱桃进价为13元/千克,试求销售利润P(元)与销售价x
(元/千克)之间的函数关系式,并求出当x取何值时,P的值最大?
(1)在如图的直角坐标系内,作出各组有序数对(x,y)所对应的点.连接各点并观察所得的图形,判断y与x之间的函数关系,并求出y与x之间的函数关系式;(2)若樱桃进价为13元/千克,试求销售利润P(元)与销售价x
(元/千克)之间的函数关系式,并求出当x取何值时,P的值最大?
| 品种 | 先期投资 | 养殖期间投资 | 产值 |
| 西施舌 | 9 | 3 | 30 |
| 对虾 | 4 | 10 | 20 |
22、(日照市2006)日照市是中国北方最大的对虾养殖产区,被国家农业部列为对虾养殖重点区域;贝类产品西施舌是日照特产.沿海某养殖场计划今年养殖无公害标准化对虾和西施舌,由于受养殖水面的制约,这两个品种的苗种的总投放量只有50吨.根据经验测算,这两个品种的种苗每投放一吨的先期投资、养殖期间的投资以及产值如下表:(单位:千元/吨)
养殖场受经济条件的影响,先期投资不超过360千元,养殖期间的投资不超过290千元.设西施舌种苗的投放量为x吨.(1)求x的取值范围;(2)设这两个品种产出后的总产值为y(千元),试写出y与x之间的函数关系式,并求出当x等于多少时,y有最大值?最大值是多少?
 产品
产品