反比例函数的性质
班级_____________ 学号__________ 姓名_____________ 成绩评定_________
一、看准了再选
1.下列函数中,是反比例函数的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2.若反比例函数![]() 的图象经过点(-1 , 2 ),则这个函数的图象一定经过点( ) A.(2,-1) B.(
的图象经过点(-1 , 2 ),则这个函数的图象一定经过点( ) A.(2,-1) B.(![]() ,2)
C.(-2,-1) D.(
,2)
C.(-2,-1) D.(![]() ,2)
,2)
3.已知反比例函数y=![]() ,若当x<0时,函数y随自变量x的增大而增大,则实数k的范围是( ). A.k≤0 B.k≥0
C.k<0
D.k>0
,若当x<0时,函数y随自变量x的增大而增大,则实数k的范围是( ). A.k≤0 B.k≥0
C.k<0
D.k>0
4.已知反比例函数y=![]() (k≠0)的图象经过点(3,4)则它的图象的两个分支分别在( ).
(k≠0)的图象经过点(3,4)则它的图象的两个分支分别在( ).
 A.第二,四象限内 B.第一,二象限内 C.第三,四象限内 D.第一,三象限内
A.第二,四象限内 B.第一,二象限内 C.第三,四象限内 D.第一,三象限内
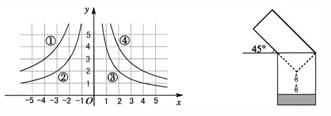
5.如图,双曲线![]() 的一个分支为( )
的一个分支为( )
A.①. B.②.C.③. D.④.
6.如图,A为反比例函数![]() 图象上一点,AB
图象上一点,AB![]()
![]() 轴与点B,
轴与点B,
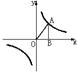 若
若![]() ,则
,则![]() 为( )A.
为( )A. ![]() B.
B. ![]() C.
C.![]() D.无法确定
D.无法确定
7.在同一直角坐标平面内,如果直线![]() 与双曲线
与双曲线![]() 没有交点,那么
没有交点,那么![]() 和
和![]() 的关系一定是( )A.
的关系一定是( )A. ![]() <0,
<0,![]() >0 B.
>0 B. ![]() >0,
>0,![]() <0 C.
<0 C.![]() 、
、![]() 同号 D.
同号 D.![]() 、
、![]() 异号
异号
8.若![]() 与-3
与-3![]() 成反比例,
成反比例,![]() 与
与![]() 成正比例,则
成正比例,则![]() 是
是![]() 的( )
的( )
A、正比例函数 B、反比例函数 C、一次函数 D、不能确定
9.若反比例函数![]() 的图像在第二、四象限,则
的图像在第二、四象限,则![]() 的值是( )
的值是( )
A、-1或1 B、小于![]() 的任意实数 C、-1 D、不能确定
的任意实数 C、-1 D、不能确定
10.函数![]() 的图象经点(1,-2),则函数y=kx+1的图象不经过( )
的图象经点(1,-2),则函数y=kx+1的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.已知点![]() 、
、![]() 、
、![]() 都在函数
都在函数![]() 的图象上,则下列关系式正确的是( )A.
的图象上,则下列关系式正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.已知一个矩形的面积为24cm2,其长为ycm,宽为xcm,则y与x之间的函数关系的图象大致是( ) D

13.直线y=2x与双曲线y=![]() 的图象的一个交点坐标为(2,4),则它们的另一个交点坐标是( ) A、(-2,-4) B、(-2,4) C、(-4,-2) D、(2,-4)
的图象的一个交点坐标为(2,4),则它们的另一个交点坐标是( ) A、(-2,-4) B、(-2,4) C、(-4,-2) D、(2,-4)
14.已知一次函数y=kx+b的图象经过第一、二、三象限,则函数y=![]() 的图象在( )
的图象在( )
A.第一、三象限 B.第二、四象限 C.第三、四象限 D.第一、二象限
15.用规格为50cm×50cm的地板砖密铺客厅恰好需要60块。如果改用规格为acm×acm的地板砖y块也恰好能密铺该客厅,那么y与a之间的关系为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
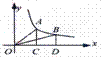 16.直线y=x与双曲线
16.直线y=x与双曲线![]() 的一个交点为A,且OA=2,则k的值为( )
的一个交点为A,且OA=2,则k的值为( )
A、1 B、2 C、![]() D、
D、![]()
17.如图,过双曲线y=(k是常数,k>0,x>0)的图象上两点A、8分别作AC⊥x轴于C,BD⊥x轴于D,则△AOC的面积S1和△BOD的面积S2的大小关系为( )
A.S1>S2 B.S1=S2 C.S1<S2 D.S1和S2的大小无法确
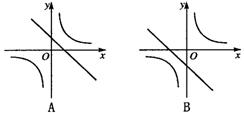
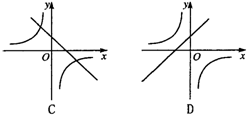
18.函数y=k(x-1)与y=-![]() 在同一直角坐标系内的图象大致是( )
在同一直角坐标系内的图象大致是( )
二、想好了再填
1.下列函数:①xy=![]() ;②y=5-x;③
;②y=5-x;③![]() ;④
;④![]() ;⑤y=-3x;其中是反比例函数的是
;⑤y=-3x;其中是反比例函数的是
2.若点![]() 在反比例函数
在反比例函数![]() 的图象上,则
的图象上,则![]()
3.若反比例函数![]() 在每个象限内y随x的增大而增大,则k= 。
在每个象限内y随x的增大而增大,则k= 。
4.若反比例函数![]() 的图象位于一、三象限内,正比例函数
的图象位于一、三象限内,正比例函数![]() 过二、四象限,则k的整数值是 。
过二、四象限,则k的整数值是 。
5.。双曲线![]() 与直线
与直线![]() 相交于A、B两点,B点坐标为(-2,-3),则A点坐标为_______________.
相交于A、B两点,B点坐标为(-2,-3),则A点坐标为_______________.
 6.点P在反比例函数y=
6.点P在反比例函数y=![]() 的图像上,若点P的纵坐标小于-1,则点P的横 坐标的取值范围是 。
的图像上,若点P的纵坐标小于-1,则点P的横 坐标的取值范围是 。
7.直线y=kx(k>0)与双曲线![]() 交于A(x1,y1),B(x2,y2)两点,则2x1y2-7x2y1的值等于__________.
交于A(x1,y1),B(x2,y2)两点,则2x1y2-7x2y1的值等于__________.
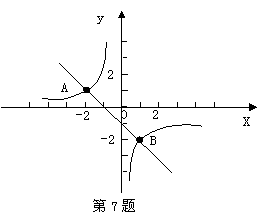
 8.如图,一次函数
8.如图,一次函数![]() 与反比例 函数
与反比例 函数![]() 的图象交于点
的图象交于点![]() ,则使
,则使![]() 的
的![]() 的取值范围是 .
的取值范围是 .
10.设有反比例函数![]() ,(
,(![]() )、
)、![]() 为其图象上两点,若
为其图象上两点,若![]() ,则k 的取值范围是
。
,则k 的取值范围是
。
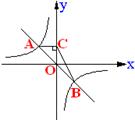
11.如图, 如果函数y=-x与y=![]() 的图像交于A、B两点, 过点A作AC垂直于y轴, 垂足为点C, 则△BOC的面积为___________.
的图像交于A、B两点, 过点A作AC垂直于y轴, 垂足为点C, 则△BOC的面积为___________.
三.想好了再规范的写
1.已知![]() 与
与![]() 成反比例,
成反比例,![]() 与
与![]() 成正比例,并且当
成正比例,并且当![]() =3时,
=3时,![]() =5,当
=5,当![]() =1时,
=1时,![]() =-1;求
=-1;求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
2.已知函数y1=x-1和y2=![]() 在同一坐标系(如下图)中画出这两个函数的图象;
在同一坐标系(如下图)中画出这两个函数的图象;
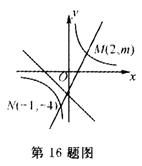
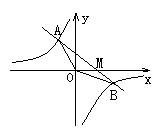
3.如图,一次函数y=-ax-b的图像与反比例函数![]() 的图象交于M、N两点.
的图象交于M、N两点.
(l)求反比例函数和一次函数的解析式;
(2)根据图像写出使反比例函数的值大于一次函数的值的x的取值范围.
 4.直线y=k1x+b与双曲线y=
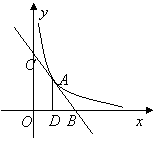
4.直线y=k1x+b与双曲线y=![]() 只有—个交点A(1,2),且与x轴、y轴分别交于B,C 两点AD垂直平分OB,垂足为D,求直线、双曲线的解析式.
只有—个交点A(1,2),且与x轴、y轴分别交于B,C 两点AD垂直平分OB,垂足为D,求直线、双曲线的解析式.
 5.已知一次函数
5.已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A,B两点,且A点的横坐标与B点的纵坐标都是
的图象交于A,B两点,且A点的横坐标与B点的纵坐标都是![]() ;(1)一次函数的解析式;(2)△AOB的面积。
;(1)一次函数的解析式;(2)△AOB的面积。