勾股定理测试题
一、填空题(每小题5分，共25分)；
1. 已知一个直角三角形的两条直角边分别为6cm，8cm，那么这个直角三角形斜边上的高为____。
2. 三角形的两边长分别为3和5，要使这个三角形是直角三角形，则第三条边长是____。
3. △ABC中，AB=10，BC=16，BC边上的中线AD=6，则AC=____。
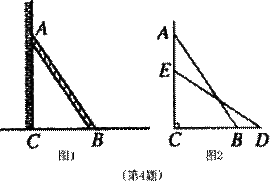
4. 如图所示，一个梯子AB长5米，顶端A靠在墙AC上，这时梯子下端B与墙角C间的距离为3米，梯子滑动后停在DE的位置上，如图2，测得DB的长为1米，则梯子顶端A下落了___米。
5. 如图将一根长24cm的筷子，置于底面直径为5cm，高为12cm的圆柱形水杯中，设筷子露在杯子外面的长度是为hcm，则h的取值范围是____。
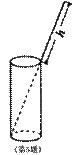
二、选择题(每小题5分，共25分)
6. 在下列以线段a，b，c的长为三边的三角形中，不能构成直角三角形的是( )
A. a=9,b=41,c=40 B. a=5,b=5,
C. a:b:c=3:4:5 D. a=11,b=12,c=15
7. 若△ABC中，AB=13，AC=15，高AD=12，则BC的长是( )
A. 14 B. 4 C. 14或4 D. 以上都不对
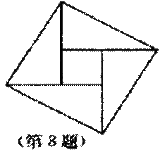
8. 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如图所示，如果大正方形的面积是13，小正方形的面积是1，直角三角形的短直角边为a，较长直角边为b，那么(a+b)2的值为( )
A. 13 B. 19 C.25 D. 169
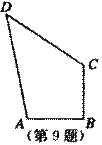
9. 如图，四边形ABCD中，AB=3cm，BC=4cm，CD=12cm，DA=13cm，且∠ABC=90°，则四边形ABCD的面积是( )
A. 84 B. 36 C. 
D. 无法确定
10. 如图，已知矩形ABCD沿着直线BD折叠，使点C落在C'处，BC'交AD于E，AD=8，AB=4，则DE的长为( )
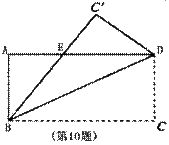
A. 3 B. 4 C. 5 D. 6
三、解答题(此大题满分50分)
11. (8分)在Rt△ABC中，∠C=90°
(1)已知c=25，b=15，求a：
(2)已知
，∠A=60°，求b，c
12. (8分)阅读下列解题过程：已知a、b、c为△ABC的三边，且满足a2c2-b2c2=a4-b4，试判断△ABC的形状。
解：
∵a2c2-b2c2=a4-b4,①
∴c2(a2-b2)=(a2+b2)(a2-b2)②
∴c2=a2+b2,③
∴△ABC为直角三角形
问：
(1)上述解题过程，从哪一步开始出现错误？请写出该步的代号_____；
(2)错误的原因是______；
(3)本题正确的结论是_____。
13. (8分)细心观察图，认真分析各式，然后解答问题：
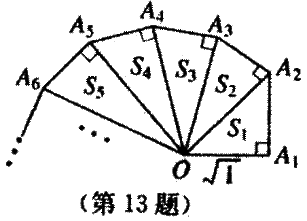
(1)用含有n(n是正整数)的等式表示上述变化规律；
(2)推算出OA10的长；
(3)求出
的值。
14. (8分)已知直角三角形的周长是
，斜边长2，求它的面积。
15. (9分)小东拿着一根长竹秆进一个宽为3米的城门，他先横着拿不进去，又竖起来拿，结果秆比城门高1米，当他把秆斜着时，两端刚好顶着城门的对角，问秆长多少米？
16. (9分)小明向西南方向走40米后，又走了50米，再走30米回到原地，小明又走了50米后向哪个方向走的？
答案：
1. 4.8cm 2. 
3. 10 4. 1 5. 11≤h≤12
6. D 7. C 8. C 9. B 10. C
11. (1)a=20 (2)
12.
(1)③ (2)a2-b2可以为0 (3)△ABC为等腰△或Rt△
13.
(1)
14. 设两直角边分别为a，b，则依题意，得：
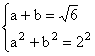
∴ab=1 
15.
设城门高为x米，则秆长(x+1)米，依题意：
x2+32=(x+1)2∴x=4故秆长5米
16. 西北方向或东南方向