初二数学竞赛模拟试题
初二数学竞赛模拟试题
一、填空题。(4分×10=40分)
1、计算π-3+π-4=_______。
2、因式分解x4+4=_______。
![]()
![]()
![]() 3、若abcd×9=dcba,则
3、若abcd×9=dcba,则![]() =_________。
=_________。
4、已知x-![]() =
=![]() ,则
,则![]() =_________。
=_________。
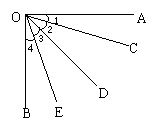 5、如图,∠1+∠4=∠2+∠3,当∠AOB=_________度时,图中所有的角的和等于一个周角。
5、如图,∠1+∠4=∠2+∠3,当∠AOB=_________度时,图中所有的角的和等于一个周角。
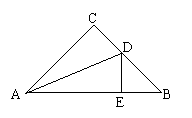
6、如图,△ABC中,∠C=90°,CA=CB,AD平分∠BAC,DE⊥AB,AB=12cm,则△BDE的周长为_________。
7、a、b、c是△ABC的三边长,若![]() ,则△ABC 是_________三角形。
,则△ABC 是_________三角形。
8、对自然数N,先写出它的所有约数,然后将这些约数两两求和,这些和中,最小的是4,最大的是2676,则N=_________。
9、方程x=kx+1的解是负数,则k的取值范围是_________。
10、对代数式(±a±b)(±a±b),当每个字母取定它前面的其中一个符号,就得到一个确定的两项式与两项式相乘的式子,如前一括号内的字母a、b分别取“+”、“-”号,后一个括号内的字母a、b分别取“-”、“+”号时,得到式子(a-b)(-a+b),那么这样的式子共能得到_________个,其中能用平方差公式计算的有_________个。
二、选择题。(4分×10=40分)
11、小明家到学校的距离为2km,小林家到学校的距离为3km,则小明家到小林家的距离不可能是( )。
A.0.5km B.1km C.2.5km D.5km
12、一个整数与它自己的和、差、积、商,这四个结果的和不可能等于( )。
A.1 B.4 C.8 D.9
13、写有数5,9,17的卡片各10张,从中选出9张,计算它们的和,这个和可能是( )。
|
14、关于x的不等式组 有5个整数解,则a的取值范围是( )。
A.-6<a<![]() B.-6≤a<
B.-6≤a<![]()
C.-6<a≤![]() D.-6≤a≤
D.-6≤a≤![]()
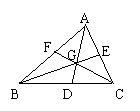 15、如图,△ABC中,中线AD,BE,CF交于点G,设△ABC的面积为1,则图中找不到下列面积的三角形( )。
15、如图,△ABC中,中线AD,BE,CF交于点G,设△ABC的面积为1,则图中找不到下列面积的三角形( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
|
|
|
|
|



|

|
|
 C.α>β D.α,β的大小不确定
C.α>β D.α,β的大小不确定
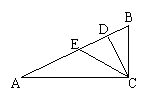
17、如图,△ABC中,∠ACB=90°,AD=AC,BE=BC,则∠DCE等于( )。
A.30° B.45° C.60° D.75°
18、某同学在探究弹簧的长度y(cm)与外力x(g)的变化关系时,实验记录得到的相应数据如表:
| 外力x(g) | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
| 指针位置y(cm) | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
|
|
|
|
|
|
|
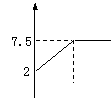
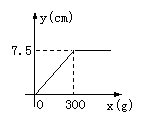 则y关于x的函数图象是( )。
则y关于x的函数图象是( )。
 | |||
 | |||
|
|
|
|
19、在等边△ABC所在的平面上,找这样的点P,使△PAB、△PBC、△PAC都是等腰三角形,这样的P点共有( )。
A.1个 B.4个 C.7个 D.10个
20、甲盒子里装有a颗白子,乙盒子里装有b颗黑子,从甲盒子中抓一把放入乙盒子中并拌匀,又从乙盒子中抓一把放入甲盒子中,这时,甲盒子中仍有a颗子,但其中混有m颗黑子,乙盒子中仍有b颗子,但其中混有n颗白子,则( )。
A.m<n B.m=n C.m>n D.m,n的大小不确定
三、解答题。(10分×4=40分)
21、长为1,2,3……9的小铜棒各一根,选择其中的若干根组成一个正方形,共有多少种不同的组法?写出各种组法的具体形式。
22、等腰△ABC中,BC上的高等于BC的一半,求∠BAC的度数。
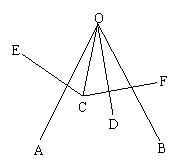 23、如图,点C,D在∠AOB内,∠AOC=∠BOD,点E,F是点D分别关于OA,OB的对称点,求证CE=CF。
23、如图,点C,D在∠AOB内,∠AOC=∠BOD,点E,F是点D分别关于OA,OB的对称点,求证CE=CF。
 24、我们知道,直角坐标系中,y=x+1表示直线
24、我们知道,直角坐标系中,y=x+1表示直线![]() ,如图(1)所示,y=
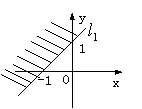
,如图(1)所示,y=![]() x+2表示直线
x+2表示直线![]() ,如图(2)所示,那么y≥x+1,则表示直线
,如图(2)所示,那么y≥x+1,则表示直线![]() 及其左上方的部分。如图(3)阴影部分,
及其左上方的部分。如图(3)阴影部分,
|
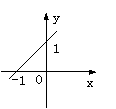 |  | ||||
![]()
![]()
![]()
![]()
|

|
|
|
|
|
|

|
|
|
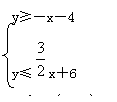 |
(1)在直角坐标系中用阴影表示出 的区域;
(2)求(1)中阴影区域的面积。
附加题:
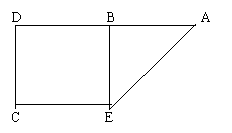
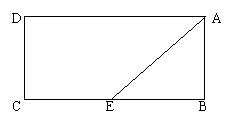
如图,一张矩形纸片ABCD,沿AE折叠,使AB重合于AD,可得∠BAE=45°,你能否也用一些矩形纸片设法折叠出一个30°的角。
(除文字说明外,也可用图来表示)
 | |||
 | |||
参考答案
一、填空题
1.1 2.(x2+2x+2)(x2+2x+2) 3.33 4.6 5.72° 6.12cm 7.等边
8.2007 9.k≥1 10.16 8
二、选择题
11.A 12.C 13.D 14.B 15.C 16.B 17.B 18.D 19.D 20.B
三、解答题
21.正方形的边长只能是7、8、9、10、11
(1)7=6+1=3+4=2+5 1种
(2)8=7+1=3+5=2+6 1种
(3)9=8+1=7+2=6+3=4+5 5种
(4)9+1=8+2=7+3=6+4 1种
(5)9+2=8+3=7+4=6+5 1种
综上所述,共9种
22.(1)当以BC为底边,∠BAC=90°;
(2)当以BC为腰,且△ABC为锐角三角形时,∠BAC=75°;
当以BC为腰,且△ABC为钝角三角形时,∠BAC=15°;
23.连结OE、OF,证△OEC≌△OFC,得OE=OF
24.(1)画图略;
(2)S阴影=30
 附加题:
附加题:
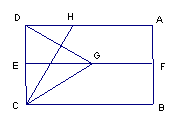
折叠AD与CB重合,得折痕EF,折叠CD,使D点落在EF上,得折痕CH,则△DCG为等边三角形,∠DCH=∠GCH=
∠GCB=∠GDA=30°。