初二数学下学期期末模拟测评卷(B)
考号＿＿＿＿＿班级＿＿＿＿＿ 姓名＿＿＿＿＿＿ 得分＿＿＿＿＿＿
一、细心填一填,相信你填得又快又准(每题3分,共30分)
1. 分式
和
的最简公分母是
2．如果
，且
，那么
3．等腰三角形的底角等于15°，腰长为2
，则腰上的高为__________________
4．化简
的结果为__________________
5. □ABCD的周长为36 cm，AB：BC＝５：７，则较长边的长为________
6. 如果一组数据-2，-1，y，3，5的平均数是1，那么y=_____, 方差是________
7. 平行四边形的周长等于56 cm，两邻边长的比为3：1，那么这个平行四边形较长的边长为_______．
8. 反比例函数
的图象经过P, 如图（1）所示, 根据图象可知, 反比例函数的解析式为______________
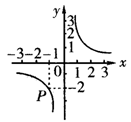
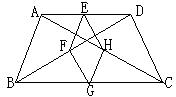
(1) (2) (3)
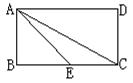
9. 如图（2），矩形ABCD中，E是BC的中点∠BAE＝30°，则AC＝
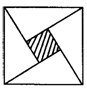
10．如图（3）是2002年8月在北京召开的第24届国际数学家大会的会标,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积为13,小正方形的面积是1,直角三角形较长的直角边为a,较短的直角边为b,则a4+b3的值等于________
二、耐心选一选,选一个你认为最适合的答案（每题3分，共30分）
11．下列判断正确的是（ ）
A、分式是有除法运算的式子 B、分式不是有理式
C、当
时，分式
的值为正 D、当
时，分式
无意义
12．关于函数y=1/x，下列结论正确的是（ ）
A、 函数图象经过点（1，1） B、函数图象经过第二、四象限
C、y随x的增大而增大 D、自变量的取值范围为 全体实数
13用两个全等的直角三角形拼下列图形：（1）平行四边形（不包含菱形、矩形、正方形）；（2）矩形；（3）菱形；（4）正方形；（5）等腰三角形．一定可以拼成的图形是（ ）
（A）（1）（2）（5） （B）（2）（3）（5）
（C）（1）（4）（5） （D）（1）（2）（3）
14． A、B、C、D在同一平面内，从①AB∥CD；②AB＝CD；③BC∥AD；④BC＝AD；这四个条件中任选两个，能使四边形ABCD成为平行四边形的选法共有（ ）
（A）3种 （B）4种 （C）5种 （D）6种
15．已知
，
，则
的值为（ ）
A、
B、
C、
D、
16．已知:ΔABC中,AB=4,AC=3,BC=5,则ΔABC的面积是( )
A.4 B.5 C.6 D.7
17．把分式
中、b都变成原来的2倍，则分式的值变为原分式值的( )
A.4倍 B.2倍 C.不变
D.
倍
18．在等腰梯形ABCD中，腰AB＝8cm，E、F、G、H
分别是AD、BD、BC、AC的中点，则四边形EFGH的
周长是 （ ）
A、15cm B、14cm C、18cm D、16cm
19．若m人需a开完成某项工程,则这样的人(m+n)个完成这项工程需要的天数是( )
A.(a+m). B.
B.
;
C.
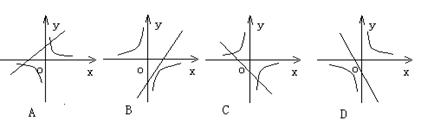
20. 一次函数y=kx-k2-1与反比例函数y=k/x在同一直角坐标系内的图象的大致位置
是图中的（ ）
三、认真算一算, 培养你的计算能力.
21．计算（3分）：
22．解分式方程（4分）：
23．先化简,后求值（4分）：
，其中
，
四、想一想，体验成功的快乐
24．（6分）某班40名学生的某次数学测验成绩统计表如下：
| 成绩（分） | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数（人） | 2 | x | 10 | y | 4 | 2 |
（1） 若这个班的数学平均成绩是69分，求x和y的值；
（2） 求这个班的数学测验成绩众数，中位数，方差；
（3）根据数据你能给这个班提出一些建议吗？
25. （5分）甲、乙两班学生同时从学校出发支距学校15千米的公园植树，乙班行走的速度是甲班的1.2倍，结果乙班比甲班先半小时到达目的地，求甲、乙两班每小时各走多少千米？
五、做一做，相信你有收获
26．（6分）如图，在RTΔABC中，∠ACB=90°，AD平分∠CAB，CE⊥AB交AD于G，DF⊥AB于F，
求证：四边形CGFD是菱形。
 |
27.（6分）如图，等腰梯形ABCD中，AD∥BC，∠DBC=45º。翻折
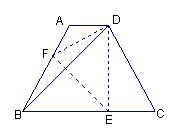梯形ABCD，使点B重合于点D，折痕分别交边AB、BC于
点F、E。若AD=2，BC=8，
求：（1）BE的长。（2）CD：DE的值。
28. （6分）如图，已知正方形ABCD中，E是BC的中点，F在CD上，且DF=3CF．
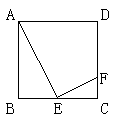求证：△ABE∽△ECF．
六、附加题: 仔细想一想,相信你一定行
29. (10分)先阅读下面的材料,然后解答问题:
通过观察，发现方程
的解为
;
的解为
;
的解为
;
…………………………
(1)观察上述方程的解,猜想关于x的方程
的解是________________;
(2)根据上面的规律,猜想关于x的方程
的解是___________________;
(3) 把关于x的方程
变形为方程的形式是________,方程的解是____________,解决这个问题的数学思想是_________________;
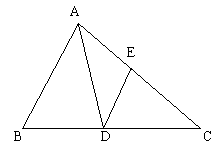
30.如图，已知△ABC中，
，∠C＝45°，BC＝6，D在BC上，DE∥AB交AC于E，设
。
（1）用x表示△ADE的面积。
（2）是否存在这样的点D使△ABD与△ADE面积相等，若存在则求出BD的长，否则说明为什么不存在？
