初二数学下学期质量抽测（一）

初二数学下学期质量抽测（一）

　　　　　　　　　　　　　　　　

一　选择题（每题3分，共30分）

1）1、下列是分式的是　 （　　　）。　　A、　　 B、　　C、　　 D、x²y²

2）下列约分正确的是　 （　　  ）A、；　B、； C、；　D、

3）如果把分式中的x和y都扩大为原来的2倍，则分式的值　　 （　　  ）

A、扩大为原来的4倍；　　 B、扩大为原来的2倍；　　 C、不变；　　  D缩小为原来的倍

4）．甲、乙两班学生参加植树造林，已知甲班每天比乙班多植5棵树，甲班植80棵树所用的天数与乙班植70棵树所用的天数相等，若设甲班每天植树x棵，则根据题意列出的方程是（　　　 ）.

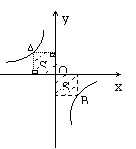（A）　（B）　（C）　 （D）

5）下列各点中，在第四象限的点是　　　　　　 （　　　　  ）

A. (2, 4)　　　　　 B. 4)　　　C.　（2，－4）　　　　D. （a²＋1，－3）

6）在直角坐标系中，点P(2,1)关于y轴对称的点的坐标是　　（　　  ）

A. (－2, 1)　　 B. (2, 1)　　　 C.(2, －1)　　　　D.(－2,－1)

7）函数y＝ －＋1和y ＝＋1的图象的交点的坐标是　(　　).　　　　

　 (A)　 ( －2，1)　　　 (B)　 (－1，3)　　　 (C) (1，0)　　(D)　　(0，1)　　

8）如上图，在函数y= －的图象上有两点A、B，过这两点分别向x轴、y轴作垂线，所作垂线与坐标轴构成的矩形的面积分别记作S_A、S_B，则S_A与S_B的大小关系是　 （　　　）

A、S_A>S_B  　　B、S_A=S_BC、S_A<S_B　 　　　　D、S_A与S_B大小关系不能确定

9）已知：在函数的图象上，则　　 （　　）

　A、； B、； C、； D、。

10) 甲、乙两同学从A地出发，骑自行车在同一条路上行驶到B地，他们离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系的图象如图所示，根据图中提供的信息，有下列说法：(　　)

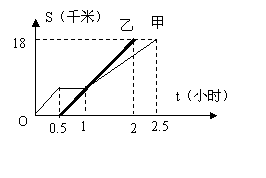（1）他们都行驶了18千米；（2）甲在途中停留了0.5小时；

（3）乙比甲晚出发了0.5小时；（4）相遇后，甲的速度小于乙的速度；

（5）甲、乙两人同时到达目的地。　

其中，符合图象描述的说法有

A.　2个　　B.　3个　　C.　4个　　 D.　5个

二　填空题（每题2分，共24分）

11．当x　　　　时，分式有意义；当x　　　　时，分式的值为零。

12．直接写出结果：  =＿＿＿＿， (02常州市) (－3)⁰＝＿＿＿＿；

13．计算：__________。

14．若解方程产生了增根，那么增根是_________.

15．已知点P（6。－8）到x轴的距离是　　　  ，到原点的距离是　　　　 。

16．已知一次函数，函数的值随值的增大而减小 ,则的取值范围是　　　 。

17．函数中自变量x的取值范围是　　　　　 .

18．一次函数y= —3x +6的图象与y轴的交点坐标是　　　　 ，与x轴的交点坐标是　　　　 。

19．直线与平行，则k=　　　　。

20．写出同时具备下列两个条件的一次函数表达式（写出一个即可）　　　　　　　  .

（1）y随着x的增大而减小。　　（2）图象经过点（1，－4）

21．一次函数y=( m + 1)x + m—2的图象不经过第三象限，则整数m是　　　　　　  。

22.如果记y= = f (x), 并且f (1) 表示 当x=1时 y 的值, 即　f (1)==;

f　() 表示 当x= 时y 的值, 即f ()==;　

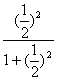那么f (1)+f (2)+f ()+f (3)+f ()+…+f (2007)+f ()=　　　　 ____　

三．解答题：本大题共8小题，共46分。解答应写出必要的计算过程或文字说明。

23．化简： （本题4分）　　　　24。化简：（本题5分）

25．解方程：（本题5分）

26．　若反比例函数y= －与一次函数y= mx－2的图象都经过点P (a,1)　　（本题6分）

求：（1）求点P坐标；　 （2）求一次函数y=mx-2的解析式；

（3）若点A（t，y₁）、B (t＋3，y₂)都在这个一次函数的图象上，试比较y₁、y₂的大小。

27．已知一次函数y＝kx＋b的图象经过点A(0,4)和点B(－1, 6) （本题6分）

(1)求一次函数的解析式，并画出它的图象．　　 （2）根据图象回答：x取何值时，y＞0。

28．昆山市出租车的收费标准如下：（6分）

里程	收费（元）
3千米以下（含3千米）	8.00
3千米以上，每增加1千米	1.80

（1）写出费用（元）与出租车行驶的里程数x（千米）之间的函数关系式；

（2）计算：乘车2.8千米，需车费　　 元，乘车10千米，需车费　　 元，

（3）画出费用（元）与出租车行驶的里程数x（千米）之间的函数的图象。

29．某空军加油飞机接到命令，立即给另一架正在飞行的飞机进行空中加油。在加油过程中，

设运输飞机的油箱余油量为吨,加油飞机的加油箱余油量为吨，加油时间为t(分)， 、

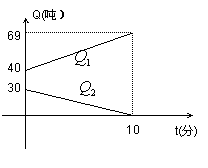
与t之间的函数图像如图所示，结合图像回答下列问题：

（1） 加油飞机的加油油箱中装载了　　 吨油，将这些油全部加给运输飞机需　　 分钟。

（2）求加油过程中，运输飞机的余油量（吨）与时间t（分）的函数关系式；

（3）运输飞机加完油后，以原速继续飞行，需10小时到达目的地，油料是否够用？说明理由。(7分)

30．仔细阅读下列材料，然后解答问题。（7分）

某商场在促销期间规定：商场内所有商品按标价的80%出售。同时当顾客在该商场消费满一定金

额后，按如下方案获得相应金额的奖券：

消费金额（元）的范围					…
获得奖卷的金额（元）	30	60	100	130	…

根据上述促销方法，顾客在商场内购物可以获得双重优惠。例如，购买标价为450元的商品，则

消费金额为元，获得的优惠额为元。设购买该商品

得到的优惠率=购买商品获得的优惠额÷商品的标价。

（1）购买一件标价为1000元的商品，顾客得到的优惠率是　　　 　 。

（2）对于标价在500元与800元之间（含500元和800元）的商品，顾客购买标价为多少元的

商品，可以得到的优惠率？