初二数学第三周周练试卷
命题人：王林 审核人：季加胜
班级 姓名 学号 得分
一、填空题 （24分）
1．
如果函数
是反比例函数，那么k=_______。
2．
已知反比例函数 
，当
时，其图象的两个分支在第一、三象限内。
3．京沪高速公路全长约为1262km，汽车沿京沪高速公路从上海驶往北京，汽车行驶完全程所需的时间t（h）与行驶的平均速度v(km/h)之间的函数关系是 。
4．已知函数
，当
时，
，则函数的解析式是
5．已知
与
成反比例，当
时，
，则
与间的函数关系式为
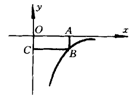6．如图，面积为3的矩形OABC的一个顶点B在反比例函数
的图象上，另三点在坐标轴上，则
=
。
二、选择题（32分）
1．下列各选项中，两个变量之间是反比例函数关系的有 （ ）A1个B2个C3个D4个
（1） 小明完成百米赛跑时，时间t(s)与他跑步的平均速度v（m/s）的之间的关系
（2） 菱形的面积为24cm2。它的两条对角线的长y（cm）与x（cm）之间的关系
（3） 某村现有耕地1000亩，该村人均占有耕地面积y（亩/人）与该村人口数量n（人）之间的关系
（4） 一个容积为20(L)的容器中,进水的时间T（）与进水的速度V（）之间的关系
2．某玩具厂计划生产一种玩具熊猫，已知每只玩具熊猫的成本为y元，若该厂每月生产 x只（x取正整数），这个月的总成本为5000元，则y与x之间满足的关系为（ ）
A 
B 
C 
D 
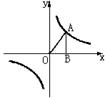3．如图，A为反比例函数
图象上一点，AB
轴与点B，若
，则为（ ）A 
B 
C 
D 无法确定
4．函数的图象经过（
，
，
则函数
的图象是 （
）
5．已知反比例函数
的图像上有两点A(
，
)，B(
，
)，且
，则
的值是 （ ）
A 正数 B 负数 C 非正数 D 不能确定
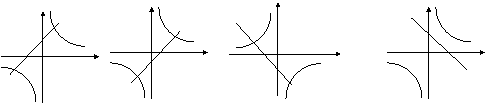6．在同一坐标系中，函数
和
的图像大致是 （ ）
A B C D
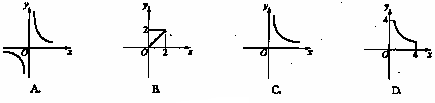7．如图，面积为2的ΔABC，一边长为，这边上的高为，则与的变化规律用图象表示大致是
（ ）
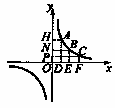8．如图所示，A（，）、B（，
）、C（
，
）是函数
的图象在第一象限分支上的三个点，且＜＜，过A、B、C三点分别作坐标轴的垂线，得矩形ADOH、BEON、CFOP，它们的面积分别为S1、S2、S3，则下列结论中正确的是
（ ）
A． S1<S2<S3 B． S3 <S2< S1
C． S2< S3< S1 D． S1=S2=S3
三、解答题：
1、已知
与成反比例，与
成正比例，并且当=3时，=5，当=1时，=-1；求与之间的函数关系式.（10）
2．如图：A，B是函数的图象上关于原点O对称的任意两点。AC平行于轴，BC平行于轴，求△ABC的面积。（10）
3．码头工人以每天30吨的速度往一艘轮船上装载货物，把轮船装载完毕恰
好用了8天时间。⑴轮船到达目的地后开始卸货，卸货速度v( 单位： 吨/天) 与卸货时间t(单位：天)之间有怎样的函数关系？⑵由于遇到紧急情况，船上的货物必须在不超过5日内卸载完毕，那么平均每天至少要卸载多少吨？
3．某气球内充满了一定质量的气体，当温度不变时，气球内的气压p(kpa)是气体体积v(m3)的反比例函数，其图象如图所示。（10）
（1）写出这一函数的表达式。（2）当气球体积1 .5m3为时，气压是多少？
（3）当气球内的气压大于144kpa时，气球将爆炸，为了安全起见，气球的体积应小于多少？
4．某商场出售一批进价为2元的贺卡，在市场营销中发现此商品的日销售单价x 元与日销售量y个之间有如下关系：
| x(元) | 3 | 4 | 5 | 6 |
| y（个） | 20 | 15 | 12 | 10 |
（1）根据表中数据，在直角坐标系中描出实数对（x,y）的对应点；
（2）猜测并确定y与x之间的函数关系式，并画出图象；
（3）设经营此贺卡的销售利润为W元，试求出W与x之间的函数关系式，若物价局规定此贺卡的销售价最高不能超过10元，请你求出当日销售单价x定为多少元时，才能使获利润最大？
5．为了预防“禽流感”，某学校在教室采用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y（ 毫克）与时间x（分钟）成正比例，药物燃烧后 ，y与 x 成反比例（如图所示）。现测得药物8分钟燃烧完毕，此时室内空气中每立方米的含药量为6毫克，请根据题中提供的信息，解答下列问题:（ 16 ）
（1）药物燃烧时， y关于 x的函数关系式为 ，自变量x的取值范围是 药物燃烧后，y关于x的函数关系式为
（２）研究表明，当空气中每立方米的含药量低于1.6毫克时学生方可进教室，那么从消毒开始，至少需要经过 分钟后，学生才能回到教室：
（３）研究表明，当空气中每立方米的含药量不低于３毫克且持续时间不低于１０分钟，才能有效杀灭空气中的病毒，那么此次消毒有效吗？为什么？