八年级数学第二次月考试卷
温馨提示：仔细审题，认真解答 满分：100分 时间：100分
班级____________姓名__________________成绩______________
一、精心选一选（每小题2分，共20分）
1、两个三角形只有以下元素对应相等，不能判定两个三角形全等的是（ ）
A. 两角和一边 B. 两边及夹角 C. 三个角 D. 三条边
2、下列说法不正确的是( )
A．条形统计图能清楚地反映出各项目的具体数量
B．折线统计图能清楚地反映事物的变化情况
C．扇形统计图能清楚地表示出各个部分在总体中所占的百分比
D．统计图只有以上三种
3、下列说法中：①如果两个三角形可以依据“AAS”来判定全等，那么一定也可以依据“ASA”来判定它们全等；②如果两个三角形都和第三个三角形不全等，那么这两个三角形也一定不全等；③要判断两个三角形全等，给出的条件中至少要有一对边对应相等．正确的是（ ）
A．①和② B．②和③ C．①和③ D．①②③
4、现有一组数据，最大值为93，最小值为22，现要把它分成6组，则下列组距中，合适的为( ) A．9 B．12 C．15 D．18
5、如图1，AD是
的中线，E，F分别是AD和AD延长线上的点，且
，连结BF，CE．下列说法：①CE＝BF；②△ABD和△ACD面积相等；③BF∥CE；④△BDF≌△CDE．其中正确的有（ ） A．1个 B．2个 C．3个 D．4个
 |
|
6、某音乐行出售三种音乐CD ，即古典音乐、流行音乐、民族音乐，为了表示这三
种音乐唱片的销售量的百分比，应该用( )
A．扇形统计图 B．折线统计图 C．条形统计图 D．以上都可以
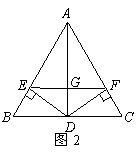
7、已知：如图2，在△ABC中，AB＝AC，D是BC的中点，DE⊥AB于E，DF⊥AC于F，则图中共有全等三角形（ ） A．5对 B．4对 C．3对 D．2对
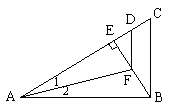
8、如图3，AB⊥BC，BE⊥AC，∠1=∠2，AD=AB，则（ ）
A. ∠1=∠EFD B. BE=EC C. BF=DF=CD D. FD∥BC
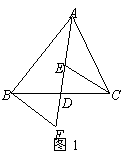
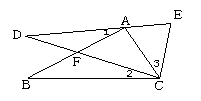
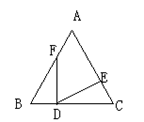
9、如图4,已知在△ABC中,AB=AC,D为BC上一点,BF=CD,CE=BD,则∠EDF等于( ) A..90°－∠A B.
90°－
∠A
C. 180°－∠A
D. 45°－∠A
10、如图5，A在DE上，F在AB上，且AC=CE，∠1＝∠2＝∠3，则DE的长等于( ) A．DC B． BC C．AB D．AE+AC
 | |||
| |||
|
二、相信你一定能填好！（每空2分，共38分）
1、函数
的自变量的取值范围为
。
2、如图6，
，
，那么只需补充一个条件
_ ，就能使
≌
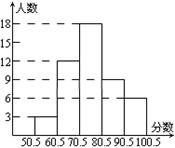
3、某地区为了增强市民的法制观念，抽调了一部分市民进行了一次知识竞赛，竞赛成绩(得分取整数)进行整理后分成五组，并绘制成频数分布直方图(如图7)，请结合直方图提供的信息填空：（1）共抽取了_______人参赛；
（2）60.5~70.5这一分数段的频数是________，频率是_____
4、已知≌，
与
是对应顶点，
与
是对应顶点，的周长
为18，
=5，
=6，则
= 。
5、2003~2005年陕西省财政收入情况如图8所示．根据图中的信息，回答：
（1）陕西省这三年平均年财政收入为____________亿元
（2）陕西省2004~2005年财政收入的年增长率约为______________（精确到1%）
（3）如果陕西省2005~2006年财政收入的年增长率与（2）中求得的年增长率基本相同，请估计陕西省2006年财政收入约为______________亿元.（精确到1亿元）
 |
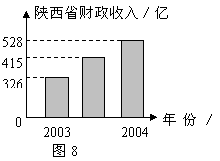| 传播途径(种) | 0 | 1 | 2 | 3 |
| 知晓人数(人) | 3 | 7 | 15 | 25 |
|
|
6、我校抽查了208班50名学生对艾滋病三种主要传播途径的知晓情况，结果如上表(如图9)：在制作扇形统计图时估计我该八年级425名学生中，三种传播途径都知道的部分扇形所对的圆心角是 。
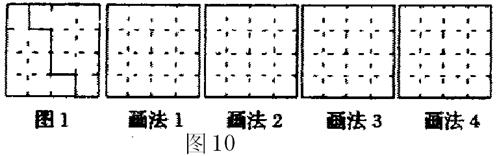7、如图10，把大小为4×4的正方形方格图形分割成两个全等图形，例如图1．请在下图中，沿着虚线画出四种不同的分法，把4×4的正方形方格图形分割成两个全等图形．
8、△ABC中，∠A＋∠B＝∠C，∠A的平分线交BC于点D，若CD＝8cm，则点D到AB的距离为________cm．
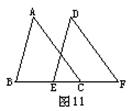
9、已知：如图11，∠ABC＝∠DEF，AB＝DE，要说明△ABC≌△DEF，
（1）若以“SAS”为依据，还须添加的一个条件为________________.
（2）若以“ASA”为依据，还须添加的一个条件为________________.
（3）若以“AAS”为依据，还须添加的一个条件为________________.
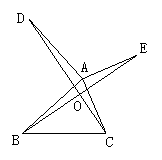10、如图12，DA⊥AB，EA⊥AC，AB＝AD，AC＝AE，BE和CD相交于O，则∠DOE的度数是 ．
|
三、认真细心作答（共40分）
1、如图，三条公路分别相交于A、B、C、三点，现要在三条公路围成的平地上建一座加油站P，加油站P到三条公路的距离相等，请你用直尺和圆规确定点P的位置。（4分）(保留作图痕迹,不写作图过程)
A
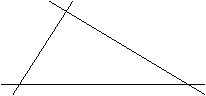
B C
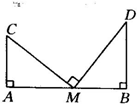
2、（8分）如图所示，两根旗杆间相距12m，某人从B点沿BA走向A，一定时间后他到达点M，此时他仰望旗杆的顶点C和D，两次视线的夹角为90°，且CM=DM，已知旗杆AC的高为3m，该人的运动速度为1m/s，求这个人运动了多长时间？
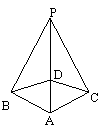3、(8分)如图，已知PB⊥AB , PC⊥AC，且PB =PC，D 是AP上的一点，
求证：
．
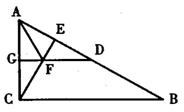
4、（10分）如图，在△ABC中，∠ACB=90°，CE⊥AB于点E，AD=AC，AF平分∠CAB交CE于点F，DF的延长线交AC于点G，求证：（1）DF∥BC；（2）FG=FE.
5、（12分）实验中学为了了解初二年级本校
名
周岁女生的身体发育状况，任意抽取了
名女生，对其身高进行测量，结果如下（数据均为整数，单位：
）：
，
，
，
，
，
，
，
，
，，
，，
，
，，
，
，，，
．
统计人员将上述数据整理后，列出了频率分布表并画出（如下图）．
| 分组 | 频数 | 频率 |
|
| 2 | 0．10 |
|
|
|
|
|
|
|
|
|
|
| D |
|
|
|
|
| 合计 |
|
|
根据以上信息回答下列问题：
（1）频率分布表中的
________，
________，
________，
________；
（2）原数据中，的值范围是____________________；
（3）该校身高在
以上（含）的周岁女生大约有________人
（4）画出频率分布直方图
附加题（20分） (1)如图１，以
的边、
为边分别向外作正方形
和正方形
，连结
，试判断与
面积之间的关系，并说明理由．
(2)园林小路，曲径通幽，如图２所示，小路由白色的正方形理石和黑色的三角形理石
铺成．已知中间的所有正方形的面积之和是
平方米，内圈的所有三角形的面积之和
是
平方米，这条小路一共占地多少平方米？（注意：解答过程写在纸上粘到试卷上）
