八年级数学秋季期末试题
一．开心选择(每小题3分，共30分)
01．下列各式由左边到右边的变形中，是分解因式的为（ ）。
A、a(x+y)=ax+ay B、x2－4x+4=x(x－4)+4
C、10x2－5x=5x(2x－1) D、x2－16+3x=(x－4)(x+4)+3x
02．下列运算中，正确的是（ ）。
A、x3·x3=x6 B、3x2+2x=5x3 C、(x2)3=x5 D、(x+y2)2=x2+y4
03．下列图形中，不是轴对称图形的是（ ）。
 |
04．已知△ABC的周长是24，且AB=AC，又AD⊥BC，D为垂足，若△ABD的周长是20，则AD的长为（ ）。
A、6 B、8 C、10 D、12
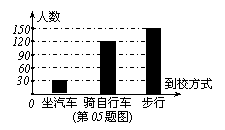
05．如图，是某校八年级学生到校方式的条形统计图，根据图形可得出步行人数占总人数的（ ）。
A、20％ B、30％ C、50％ D、60％
06．已知一次函数y=kx－k，若y随着x的增大而减小，则该函数的图象经过（ ）。
A、第一、二、三象限 B、第一、二、四象限
C、第二、三、四象限 D、第一、三、四象限
07．已知等腰三角形一边长为4，一边的长为6，则等腰三角形的周长为 ）。
A、14 B、16 C、10 D、14或16
08．已知xm=6，xn=3，则x2m－3n的值为（ ）。
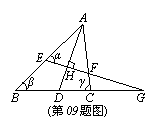A、9 B、
C、2 D、
09．如图，AD平分∠BAC，EG⊥AD于H，则下列等式中成立的是（ ）。
A、∠α=
(∠β+∠γ) B、∠α=(∠β－∠γ)
C、∠G=(∠β+∠γ) D、∠G=∠α
10．直线y=x－1与两坐标轴分别交于A、B两点，点C在坐标轴上，若△ABC为等腰三角形，则满足条件的点C最多有（ ）。
A、4个 B、5个 C、7个 D、8个
二．快乐填空 (每小题4分，共32分)
11．已知am·a3＝a10，则m＝ 。
12．分解因式x3y3－2x2y2＋xy＝ 。
13．若函数y＝4x＋3－k的图象经过原点，那么k＝ 。
14．如图，一艘轮船向正东方向航行，上午9时测得它在灯塔P的南偏西
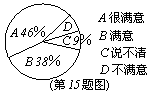
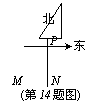
30°方向，距离灯塔120海里的M处，上午11时到达这座灯塔的正南方向的N处，则这艘轮船在这段时间内航行的平均速度是 海里。
15．某商场为了解本商场的服务质量，随机调查了本商场的100名顾客，调查的结果如图，根据图中给出的信息，这100名顾客中对该商场的服务质量表示不满意的有 人。
16．已知x＋y＝1，则x2＋xy＋y2＝ 。
17．三角形的三条边长分别为3cm、5cm、xcm，则此三角形的周长y(cm)与x(cm)的函数关系式是 ；
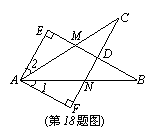
18．如图EB交AC于M，交FC于D，AB交FC于N，∠E＝∠F＝90°，∠B＝∠C，AE＝AF。给出下列结论：①∠1＝∠2；②BE＝CF；③△ACN≌△ABM；④CD=DN。其中正确的结论有 (填序号)。
三．认真解答，一定要细心哟！（共88分)
19．(8分)分解因式
20．(8分)先化简，再求值：a+b=6,ab=2.(1)求
的值
21．(每小题6分，共12分)把下列各式分解因式：
(1)1+m+
(2)(x2+y2)2-4x2y2
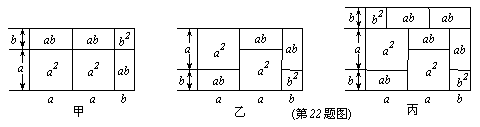
22．(8分)阅读理解题：我们已经接触了一些代数恒等式，并且可以用长方形的面积来解释这些代数恒等式。例如：(2a+b)(a+b)=2a2+3ab+b2就可以用下图中的图甲或图乙等图形的面积来解释。
(1)请写出图丙所对应的代数恒等式： ；
(2)请仿照上述方法另写一个含有a、b的代数恒等式，并画出与之对应的几何图形。
 |
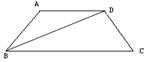
23．
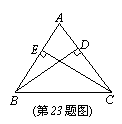(8分)如图，已知△ABC，BD⊥AC于D，CE⊥AB于E，请你增加一个条件，写出一个结论，并证明你写出的结论。(不再增加辅助线)
你增加的一个条件是： 。
你给出的一个结论是： 。
 |
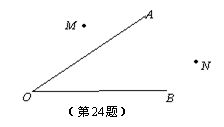24、（8分）已知：∠AOB, 点M、N.
求作：点P,使点P在∠AOB的平分线上,且PM=PN.
（要求：用尺规作图,保留作图痕迹,不写作法）
25、某产品每件成本10元，试销阶段每件产品的日销售价
（元）与产品的日销售量
（件）之间的关系如下表：（10分）
|
| 15 | 20 | 25 | 30 | … |
|
| 25 | 20 | 15 | 10 | … |
（1）
请在直角坐标系上描点，观察点的颁布，建立与的恰当函数模型。
（2） 若要求每天卖出24件，则这一天它能获利多少元？
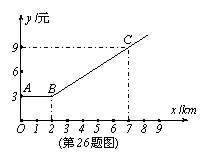
26．(12分)如图，折线A－B－C是某市区出租汽车所收费用y(元)与出租车行驶路程x(km)之间的函数关系的图象。根据图象，求：
(1)当x≥2时，y与x之间的函数关系式；
(2)某人乘车0.5km应付车费多少元？
(3)某人付车费15.6元，则出租车行走了多少千米？
 |
27．(14分)在Rt△ABC中，AB＝AC，∠BAC=90°，O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系(不要求证明)；
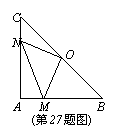(2)如果点M、N分别在线段AB、AC上移动，在移动中保持AN＝BM，请判断△OMN的形状，并证明你的结论。