八年级数学下册期末综合检测题（人教版）
四川省合江县焦滩中学 赵世江
班级：＿＿＿＿＿ 姓名：＿＿＿＿＿＿＿ 得分：＿＿＿ 等级：＿＿＿
A 卷（100分）
一、选择题（每小题4分，共48分）
1、下列说法正确的是（ ）
（A）3是9的平方根 （B）-9的平方根是±3
（C）4的平方根是2 （D）(-5)2的算术平方根是 -5
2、在实数范围内0，-4，8，(-7)2有平方根的有（ ）
（A）1个 （B）2个 （C）3个 （D）4个
3、(
)2等于（ ）
（A）20 （B）-200 （C）200 （D）-20
4、点P(
)关于x轴对称与关于y轴对称的点的坐标相同，则
的值分别是（ ）
（A） –1, 2 （B） –1, –2 （C） –2, 1 （D） 1, 2
5、四边形中，若一组对角都是直角，则另一组对角可以是（ ）
（A）都是钝角 （B）都是锐角 （C）一个直角和一个锐角 （D）一个锐角和一个钝角
6、有下面命题：
①直角三角形的两个锐角互余
②钝角三角形的两个内角互补
③正方形的两条对角线相等
④菱形的两条对角线互相垂直.
其中，正确的命题有（ ）
（A）1个（B）2个（C）3个（D）4个
7、如果
有意义，则
的取值范围为（ ）
（A）<2（B）≤2（C）>-2且≠-1（D）≤2且≠-1
8、下列语句中正确的是（ ）
| |
(C)两个无理数的商一定是无理数 (D)实数
的倒数一定是
| |
| |
（B）n边形的内角和总大于外角和
|
|
|
（D）当多边形的边数增加时，它的内角和与外角和都增加
10、 ABCD的对角线AC、BD相交于点O，
|
|
（A） 2对 （B）3对 （C）4对 （D）5对 （10题图）
11、下列性质中，矩形不一定具有的是 ( )
| |
| |
| |
| |
二、填空题（每小题4分，共16分）
1、
计算：
-(
)=
2、 平行四边形ABCD的周长等于56cm，两邻边的长的比为3:1，那么这个平行四边形较长的边长为
3、 如果梯形的上底为4，下底为6，高为2，那么这个梯形的面积为
4、 矩形的一条边长为4cm，面积为20cm2，这个矩形的一条对角线的长为
三、计算（每小题4分，共16分）
1、
2、(
+
)×
3、(
-
)(
) 4、
+
+
|
的周长比 ABCD的周长少1.5cm.求平行四边形各边的长.
五、（本题6分）已知一次函数y=kx+b的图象经过点(-1, -5),且与正比例函数y= x的图象相交于点(2,a),求
(1)a的值
(2)k,b的值
(3)这两个函数图象与x轴所围成的三角形面积.
六、（本题8分）如图，梯形ABCD，AD∥BC，AB=AD+BC，E是CD的中点.
求证：（1）AE⊥BE；
|
 |
B 卷（50分）
一、填空题（每空3分，共18分）
1、 若 
<-6，化简
=
2、 已知
=0，则
的值为
3、 等腰梯形的腰长为2，下底为6，腰与下底的夹角为45º，则梯形的上底长为
4、 菱形的面积为50cm2，一个内角为30º，则其边长为
5、 已知平行四边形两邻边上的高分别为3，4，周长为21，则这个平行四边形的面积
|
|
为
| |
|
| |
6、如图，正方形ABCD的边长为1，EF分别
|
|
|
，
则ΔEAF的面积为 （6题图）
二、（本题6分）（利用
解决本题）
已知ΔABC的三边分别为a、b、c，化简：
+
+
三、（本题6分）如图，在等腰梯形ABCD中，AB∥CD，∠ABC=60º，AC平分∠DAB，
E、F分别为对角线AC、DB的中点，且EF=4.求这个梯形的面积.
|
四、（本题6分）某医药研究所开发了一种新药，在试验药效时发现，如果成人按规定剂量服用，那么服药后2小时时血液中含药量最高，达每毫升6微克，接着逐步衰减，10小时血液中含药量为每毫升3微克，每毫升血液中含药量y微克随时间x小时主变化如图所示,当成人按规定剂是服药后,
(1)分别求出x<2和x>2时y与x的函数关系式,
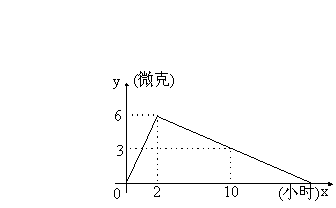(2)如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的,那么这个有效时间是多长?
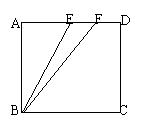
五、（本题6分）如图，在正方形ABCD中，E为AD的中点，F为ED的中点.
求证：∠ABE=
∠FBC
 |
六、（本题8分）已知正方形ABCD中，M是AB的中点，E是AB延长线上一点，
MN⊥DM且交∠CBE的平分线于N（如图1）.
|
|
（图1）
（2）若将上述条件中的“M是AB的中点”改为“M是AB
|
 |
（图2）