八年级数学（下）
第四章《相似图形》测试题
姓名___________ 班级__________ 分数_________
一、选择题（8×3′=24′）
1、下列说法“①凡正方形都相似；②凡等腰三角形都相似；③凡等腰直角三角形都相似；④直角三角形斜边上的中线与斜边的比为1∶2；⑤两个相似多边形的面积比为4∶9，则周长的比为16∶81.”中,正确的个数有（ ）个
A、1 B、2 C、3 D、4
2、在坐标系中,已知A（-3，0），B（0，-4），C（0，1）,过点C作直线L交x轴于点D,使得以点D、C、O为顶点的三角形与△AOB相相似,这样的直线一共可以作出（ ）条. A、6 B、3 C、4 D、5
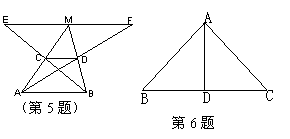
3、RtDABC中，CD是斜边AB上的高，∠BAC的平分线分别交BC、CD于点E、F。图中共有8个三角形，如果把一定相似的三角形归为一类，那么图中的三角形可分为（ ）类。 A．2 B．3 C．4 D．5
 | |||||
 | |||||
 | |||||
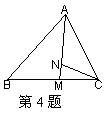
4、如图，点M在BC上，点N在AM上，CM=CN，
，下列结论正确的是（ ）
A．DABM∽DACB B．DANC∽DAMB C．DANC∽DACM D． DCMN∽DBCA
5、在梯形ABCD中，AB∥CD，AB=a，CD=b，两腰延长线交于点M，过M作DC的平行线，交AC、BD延长线于E，EF等于（ ）
A．
B．
C．
D．
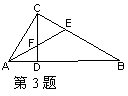
6、如图，△ABC中，AD⊥BC于D，下列条件：⑴∠B＋∠DAC＝90°；⑵∠B＝∠DAC；⑶=；⑷
其中一
定能够判定△ABC是直角三角形的有（ ）
A、1 B、2 C、3 D、4
7、如图，D、E分别是△ABC的边AB、AC上的点，
∠1＝∠B，AE＝EC＝4，BC＝10，AB＝12，
则△ADE和△ACB的周长之比为（ ） A、 B、 C、 D、
8、在△ABC与△
中，有下列条件：①
；⑵
③∠A＝∠
；④∠C＝∠
。如果从中
任取两个条件组成一组，那么能判断
△ABC∽△的共有（ ）组。
A、1 B、2 C、3 D、4
二、填空题（9×3′=27′）
9、设==，则=______，=______.
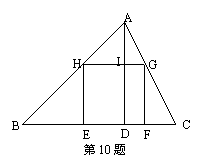
10、如图，四边形EFGH是DABC内接正方形，BC=21cm，高AD=15cm，则内接正方形边长EF=____________。
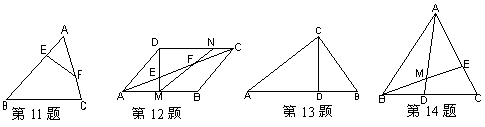
11、如图，要使DAEF和DACB相似，已具备条件__________________，还需补充的条件是_________，或_________，或_________。
12、平行四边形ABCD中，AB=28，E、F是对角线AC上的两点，且AE=EF=FC，DE交AB于点M，MF交CD于点N，则CN=_________。
13、RTDABC中，AC⊥BC，CD⊥AB于D，AC=8，BC=6，则AD=_________。
14、已知：AM：MD=4：1，BD：DC=2：3，则AE：EC=_________。
 |
15、如图，C为线段AB上的一点，△ACM、△CBN都是等边三角形，若AC＝3，
BC＝2，则△MCD与△BND的面积比为
。
16、如图，在梯形ABCD中，AD∥BC，AC、BD交于O点，S△AOD:S△COB＝1:9，
则S△DOC:S△BOC＝
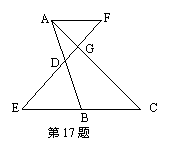
17、如图,已知点D是AB边的中点,AF∥BC,CG∶GA=3∶1,BC=8,则AF＝
三、解答题（共69分）
18、（6′）已知：平行四边形ABCD，E是BA延长线上一点，CE与AD、BD交于G、F，求证：
。
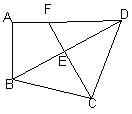
19、（8′）如图：四边形ABCD中，∠A=∠BCD=90°，①过C作对角线BD的垂线交BD、AD于点E、F，求证：
；②如图：若过BD上另一点E作BD的垂线交BA、BC延长线于F、G，又有什么结论呢？你会证明吗？
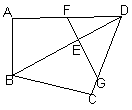
20、（6′）如图，在△ABC中，DE∥BC，且S△ADE :S四边形BCED＝1:2，BC＝2
。
求DE的长。
21、（6′）如图，矩形EFGH内接于△ABC，AD⊥BC于点D，交EH于点M，BC＝10㎝，AM＝8㎝，S△ABC＝100㎝2。求矩形EFGH的面积。
22、（6′）已知：如图，△ABC中，AE＝CE，BC＝CD，求证：ED＝3EF。
23、（6′）已知：如图，在△ABC中，∠BAC＝900，AD⊥BC于D，E是AB上一点，AF⊥CE于F， AD交CE于G点，求证：∠B＝∠CFD
 |
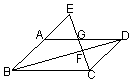
24、（6′）已知：如图，∠BDC＝∠CEA＝∠FGB，求证：BE·BA＋CD·CA＝BC2
25、（9′）矩形ABCD中，AB＝4，BC＝6，M是BC的中点，DE⊥AM，E是垂足。①求△ABM的面积；②求DE的长；③求△ADE的面积。
26、（8′）如图：△PQR是等边三角形，∠APB＝120°（1）求证：QR2＝AQ·RB
（2）若AP＝
，AQ＝2，PB＝
。求RQ的长和△PRB的面积。
 |
27、（8′）如图，矩形ABCD中，CH⊥BD，垂足为H，P点是AD上的一个动点（P与A、D不重合），CP与BD交于E点。已知CH＝
，DH∶CD＝5∶13，设AP＝
，四边形ABEP的面积为
。（1）求BD的长；（2）用含的代数式表示。
 |